第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
12. 课题学习“$ An $ 系列纸”的研究:
纸张尺寸是将纸张的长宽规范成固定的比例尺寸来使用. 目前国际最常使用的是 $ ISO $ 所制定的标准,并将尺寸冠以编号,例如 $ A4 $,$ B5 $ 等. 在不同年代,全球各地也有当地通用的纸张尺寸. 在书籍、卡片、信封以及日常书写用纸上,使用统一的纸张尺寸大大提高了生活的便利性.
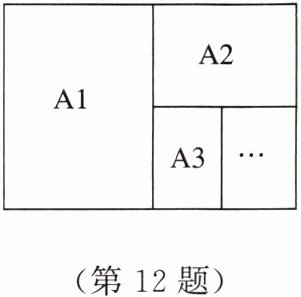
如图,$ An $ 系列矩形纸张的规格特征:①各矩形纸张都相似;② $ A1 $ 纸对裁后可以得到两张 $ A2 $ 纸,$ A2 $ 纸对裁后可以得到两张 $ A3 $ 纸……$ An $ 纸对裁后可以得到两张 $ A(n + 1) $ 纸.
(1) 填空:$ A1 $ 纸面积是 $ A2 $ 纸面积的
(2) 根据 $ An $ 系列纸张的规格特征,求出该系列纸张的长与宽(长大于宽)之比.
纸张尺寸是将纸张的长宽规范成固定的比例尺寸来使用. 目前国际最常使用的是 $ ISO $ 所制定的标准,并将尺寸冠以编号,例如 $ A4 $,$ B5 $ 等. 在不同年代,全球各地也有当地通用的纸张尺寸. 在书籍、卡片、信封以及日常书写用纸上,使用统一的纸张尺寸大大提高了生活的便利性.
如图,$ An $ 系列矩形纸张的规格特征:①各矩形纸张都相似;② $ A1 $ 纸对裁后可以得到两张 $ A2 $ 纸,$ A2 $ 纸对裁后可以得到两张 $ A3 $ 纸……$ An $ 纸对裁后可以得到两张 $ A(n + 1) $ 纸.
(1) 填空:$ A1 $ 纸面积是 $ A2 $ 纸面积的
2
倍,$ A2 $ 纸周长是 $ A4 $ 纸周长的2
倍;(2) 根据 $ An $ 系列纸张的规格特征,求出该系列纸张的长与宽(长大于宽)之比.

解:设 A1 纸的长和宽分别是 m,n,则 A2 纸的长和宽分别为 n,$\frac{1}{2}m$,$\therefore \frac{m}{n}=\frac{n}{\frac{1}{2}m}$,即$\frac{m}{n}=\sqrt{2}$,$\therefore$该系列纸张的长与宽(长大于宽)之比为$\sqrt{2}:1$.
答案:
解:
(1)2 2
(2)设 A1 纸的长和宽分别是 m,n,则 A2 纸的长和宽分别为 n,$\frac{1}{2}m$,$\therefore \frac{m}{n}=\frac{n}{\frac{1}{2}m}$,即$\frac{m}{n}=\sqrt{2}$,$\therefore$该系列纸张的长与宽(长大于宽)之比为$\sqrt{2}:1$.
(1)2 2
(2)设 A1 纸的长和宽分别是 m,n,则 A2 纸的长和宽分别为 n,$\frac{1}{2}m$,$\therefore \frac{m}{n}=\frac{n}{\frac{1}{2}m}$,即$\frac{m}{n}=\sqrt{2}$,$\therefore$该系列纸张的长与宽(长大于宽)之比为$\sqrt{2}:1$.
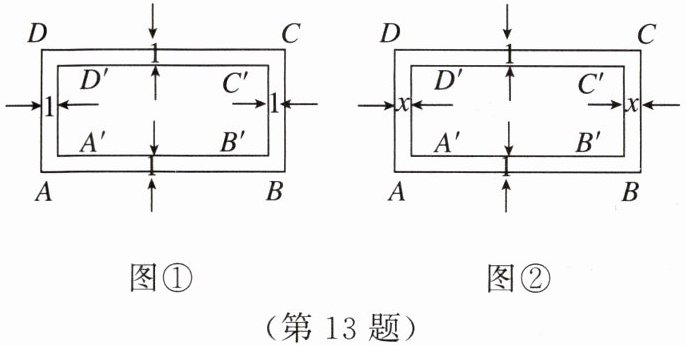
13. 如图,矩形 $ ABCD $ 的长 $ AB = 30 $,宽 $ BC = 20 $.
(1) 如图①,若沿矩形 $ ABCD $ 四周有宽为 $ 1 $ 的环形区域,图中所形成的矩形 $ ABCD $ 与矩形 $ A^{'}B^{'}C^{'}D^{'} $ 相似吗?请说明理由.
(2) 如图②,$ x $ 为多少时,图中的矩形 $ ABCD $ 与矩形 $ A^{'}B^{'}C^{'}D^{'} $ 相似?
(1) 如图①,若沿矩形 $ ABCD $ 四周有宽为 $ 1 $ 的环形区域,图中所形成的矩形 $ ABCD $ 与矩形 $ A^{'}B^{'}C^{'}D^{'} $ 相似吗?请说明理由.
(2) 如图②,$ x $ 为多少时,图中的矩形 $ ABCD $ 与矩形 $ A^{'}B^{'}C^{'}D^{'} $ 相似?

答案:
解:
(1)不相似.理由如下:$AB=30$,$A'B'=28$,$BC=20$,$B'C'=18$,$\because \frac{28}{30}\neq \frac{18}{20}$,$\therefore$两个矩形不相似.
(2)矩形 ABCD 与矩形$A'B'C'D'$相似,则$\frac{A'B'}{AB}=\frac{B'C'}{BC}$或$\frac{A'B'}{BC}=\frac{B'C'}{AB}$,则$\frac{30-2x}{30}=\frac{20-2}{20}$或$\frac{30-2x}{20}=\frac{20-2}{30}$,解得$x=1.5$或$x=9$,所以当$x=1.5$或$x=9$时,图中的矩形ABCD与矩形$A'B'C'D'$相似.
(1)不相似.理由如下:$AB=30$,$A'B'=28$,$BC=20$,$B'C'=18$,$\because \frac{28}{30}\neq \frac{18}{20}$,$\therefore$两个矩形不相似.
(2)矩形 ABCD 与矩形$A'B'C'D'$相似,则$\frac{A'B'}{AB}=\frac{B'C'}{BC}$或$\frac{A'B'}{BC}=\frac{B'C'}{AB}$,则$\frac{30-2x}{30}=\frac{20-2}{20}$或$\frac{30-2x}{20}=\frac{20-2}{30}$,解得$x=1.5$或$x=9$,所以当$x=1.5$或$x=9$时,图中的矩形ABCD与矩形$A'B'C'D'$相似.
查看更多完整答案,请扫码查看


