《2025年配套综合练习甘肃九年级数学上册北师大版》

4. 已知在$\triangle ABC和\triangle DEF$中,$\angle A = 40^{\circ}$,$\angle B = 80^{\circ}$,$\angle E = 80^{\circ}$. 当$\angle F = $60°时,$\triangle ABC\backsim\triangle DEF$.

答案： 60°

5. 如图,在四边形$ABCD$中,$\angle B = \angle ACD$,$AB = 6$,$BC = 4$,$CA = 5$,$DC = 7.5$,则$AD$的长为$\frac{25}{4}$.
]

答案： $\frac{25}{4}$

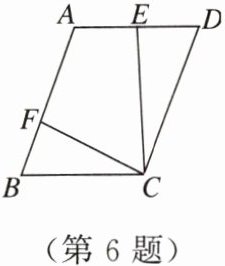
6. 如图,在$□ ABCD$中,$AB = 10$,$AD = 6$,点$E是AD$的中点,在$AB上取一点F$,使$\triangle CBF\backsim\triangle CDE$,则$BF$的长是1.8.
]

答案： 1.8

7. 如图,在$7×12$的正方形网格中有一只可爱的小狐狸,观察画面中由灰色阴影组成的五个三角形,则相似三角形有(C).

A.4 对
B.3 对
C.2 对
D.1 对
]

答案： C

8. 如图,$\triangle ABC的顶点A是线段PQ$的中点,$PQ// BC$,连接$PC$,$QB$,分别交$AB$,$AC于点M$,$N$,连接$MN$. 若$MN = 1$,$BC = 3$,则线段$PQ = $3.
]

答案： 3

9. 如图,在矩形$ABCD$中,点$E是AD$的中点,$EF\perp EC交AB于点F$,连接$FC$,$AB＞AE$.
(1)$\triangle AEF与\triangle EFC$是否相似？若相似,证明你的结论；若不相似,请说明理由.
(2)设$\frac{AB}{BC}= k$,是否存在这样的$k$值,使得$\triangle AEF与\triangle BFC$相似？若存在,证明你的结论并求出$k$的值；若不存在,请说明理由.
]

答案： 解:
(1)相似.
证明:延长FE与CD的延长线交于点G(图略).
∵点E是AD的中点，
∴AE=ED.
在Rt△AEF与Rt△DEG中，
$\left\{\begin{array}{l} ∠A=∠EDG=90^{\circ },\\ AE=DE,\\ ∠AEF=∠DEG,\end{array}\right. $
∴△AEF≌△DEG(ASA),
∴FE=GE.又CE⊥FG,
∴FC=GC,
∴∠EFC=∠G.
∵AB//CD,
∴∠AFE=∠G.
∴∠AFE=∠EFC.
又
∵∠A=∠CEF,
∴△AEF∽△ECF.
(2)存在.
分两种情况:
①当∠BCF=∠AFE时，
∵∠BCF+∠BFC = 90°,
∴∠AFE+∠BFC = 90°,
此时∠EFC=180°−(∠AFE+∠BFC)=180°−90°=90°,而∠FEC=90°,故∠EFC = 90°不存在.
②当∠BCF=∠AEF时,设AD=BC=a,AB=CD=b.
∵点E是AD的中点，
∴AE=ED=$\frac{a}{2}$.
∵△AEF∽△DCE,
∴$\frac{AE}{DC}=\frac{AF}{ED}$，即$\frac{\frac{a}{2}}{b}=\frac{AF}{\frac{a}{2}}$，
∴AF=$\frac{a^{2}}{4b}$，BF=AB - AF=b - $\frac{a^{2}}{4b}$.
∵△AEF∽△BCF,
∴$\frac{AF}{AE}=\frac{BF}{BC}$，
即$\frac{\frac{a^{2}}{4b}}{\frac{a}{2}}=\frac{b-\frac{a^{2}}{4b}}{a}$，
∴3a²=4b²，$\frac{b^{2}}{a^{2}}=\frac{3}{4}$，$\frac{b}{a}=\frac{\sqrt{3}}{2}$.
k=$\frac{AB}{BC}=\frac{b}{a}=\frac{\sqrt{3}}{2}$.
综上所述，k=$\frac{\sqrt{3}}{2}$.