第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
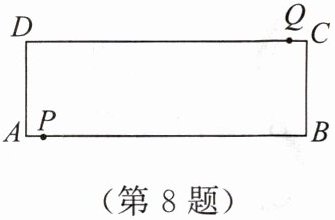
8. 如图,在矩形 $ABCD$ 中,$AB = 24\ cm$,$BC = 8\ cm$,点 $P$ 从点 $A$ 开始沿折线 $A - B - C - D$ 以 $4\ cm/s$ 的速度移动,点 $Q$ 从点 $C$ 开始沿 $CD$ 边以 $2\ cm/s$ 的速度移动,如果点 $P$,$Q$ 分别从点 $A$,$C$ 同时出发,当其中一点到达点 $D$ 时,另一点也随之停止运动. 设运动时间为 $t(s)$,当 $t$ 为多少时,四边形 $QPBC$ 为矩形?

答案:
解:
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD//AB,
∴只有CQ=BP时,四边形QPBC是矩形.由题意得CQ=2t cm,AP=4t,则BP=(24-4t)cm,
∴2t=24-4t,
∴t=4,即当t为4时,四边形QPBC为矩形.
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD//AB,
∴只有CQ=BP时,四边形QPBC是矩形.由题意得CQ=2t cm,AP=4t,则BP=(24-4t)cm,
∴2t=24-4t,
∴t=4,即当t为4时,四边形QPBC为矩形.
9. 阅读下面的材料.
在数学课上,老师请同学们思考如下问题:如图①,我们把一个四边形 $ABCD$ 的四边中点 $E$,$F$,$G$,$H$ 依次连接起来得到的四边形 $EFGH$ 是平行四边形吗?
小敏在思考问题时,有如下思路:连接 $AC$.
```
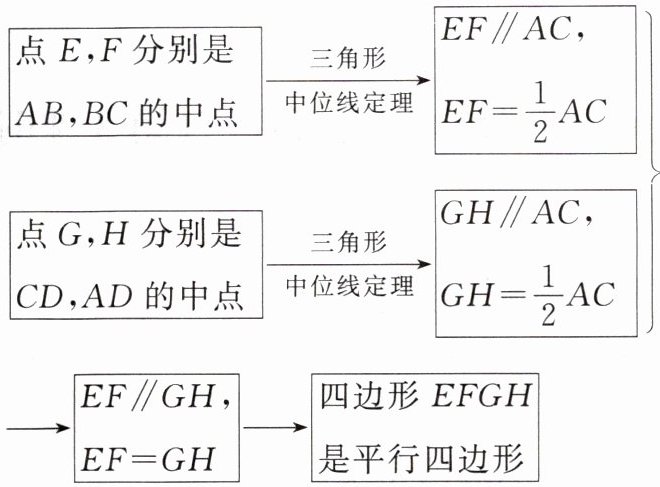
点 E,F 分别是 AB,BC 的中点 → 三角形中位线定理 → EF//AC, EF = 1/2 AC
点 G,H 分别是 CD,AD 的中点 → 三角形中位线定理 → GH//AC, GH = 1/2 AC
→ EF//GH, EF = GH → 四边形 EFGH 是平行四边形
```
结合小敏的思路作答:
(1) 若只改变图①中四边形 $ABCD$ 的形状(如图②),则四边形 $EFGH$ 还是平行四边形吗? 请说明理由.
(2) 如图②,在(1)的条件下,若连接 $AC$,$BD$.
①当 $AC$ 与 $BD$ 满足什么条件时,四边形 $EFGH$ 是菱形? 写出结论并证明.
②当 $AC$ 与 $BD$ 满足什么条件时,四边形 $EFGH$ 是矩形? 直接写出结论.

在数学课上,老师请同学们思考如下问题:如图①,我们把一个四边形 $ABCD$ 的四边中点 $E$,$F$,$G$,$H$ 依次连接起来得到的四边形 $EFGH$ 是平行四边形吗?
小敏在思考问题时,有如下思路:连接 $AC$.
```
点 E,F 分别是 AB,BC 的中点 → 三角形中位线定理 → EF//AC, EF = 1/2 AC
点 G,H 分别是 CD,AD 的中点 → 三角形中位线定理 → GH//AC, GH = 1/2 AC
→ EF//GH, EF = GH → 四边形 EFGH 是平行四边形
```
结合小敏的思路作答:

(1) 若只改变图①中四边形 $ABCD$ 的形状(如图②),则四边形 $EFGH$ 还是平行四边形吗? 请说明理由.
(2) 如图②,在(1)的条件下,若连接 $AC$,$BD$.
①当 $AC$ 与 $BD$ 满足什么条件时,四边形 $EFGH$ 是菱形? 写出结论并证明.
②当 $AC$ 与 $BD$ 满足什么条件时,四边形 $EFGH$ 是矩形? 直接写出结论.

答案:
解:
(1)四边形EFGH还是平行四边形.理由如下:连接AC.
∵E,F分别是AB,BC的中点,
∴EF//AC,EF=1/2AC.
∵G,H分别是CD,AD的中点,
∴GH//AC,GH=1/2AC,
∴EF//GH,EF=GH,
∴四边形EFGH是平行四边形.
(2)①当AC=BD时,四边形EFGH是菱形.证明如下:由
(1)可知四边形EFGH是平行四边形,当AC=BD时,FG=1/2BD,EF=1/2AC,
∴FG=EF,
∴四边形EFGH是菱形.②当AC⊥BD时,四边形EFGH是矩形.
(1)四边形EFGH还是平行四边形.理由如下:连接AC.
∵E,F分别是AB,BC的中点,
∴EF//AC,EF=1/2AC.
∵G,H分别是CD,AD的中点,
∴GH//AC,GH=1/2AC,
∴EF//GH,EF=GH,
∴四边形EFGH是平行四边形.
(2)①当AC=BD时,四边形EFGH是菱形.证明如下:由
(1)可知四边形EFGH是平行四边形,当AC=BD时,FG=1/2BD,EF=1/2AC,
∴FG=EF,
∴四边形EFGH是菱形.②当AC⊥BD时,四边形EFGH是矩形.
查看更多完整答案,请扫码查看


