第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
8. 某奥体中心的示意图如图所示,其东、西面各有一个入口 $ A $,$ B $,南面为出口 $ C $,北面分别有两个出口 $ D $,$ E $。聪聪若任选一个入口进入,再任选一个出口离开,那么他从入口 $ A $ 进入并从北面出口离开的概率为(
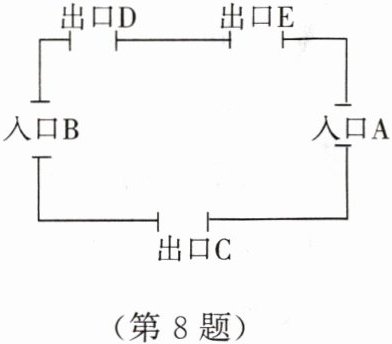
A.$ \dfrac{1}{6} $
B.$ \dfrac{1}{5} $
C.$ \dfrac{1}{3} $
D.$ \dfrac{1}{2} $
C
)。
A.$ \dfrac{1}{6} $
B.$ \dfrac{1}{5} $
C.$ \dfrac{1}{3} $
D.$ \dfrac{1}{2} $
答案:
C
9. 点 $ P $ 的坐标是 $ (a,b) $,从 $ -2 $,$ -1 $,$ 0 $,$ 1 $,$ 2 $ 这五个数中任取一个数作为 $ a $ 的值,再从余下的四个数中任取一个数作为 $ b $ 的值,则点 $ P(a,b) $ 在平面直角坐标系中第二象限内的概率是
$\frac{1}{5}$
。
答案:
$\frac{1}{5}$
10. 如图,管中放置着三根同样的绳子 $ AA_{1} $,$ BB_{1} $,$ CC_{1} $。
(1)小明从这三根绳子中随机选一根,恰好选中绳子 $ AA_{1} $ 的概率是多少?
(2)小明先从左端 $ A $,$ B $,$ C $ 三个绳头中随机选两个打一个结,再从右端 $ A_{1} $,$ B_{1} $,$ C_{1} $ 三个绳头中随机选两个打一个结,求这三根绳子能连接成一根长绳的概率。

(1)小明从这三根绳子中随机选一根,恰好选中绳子 $ AA_{1} $ 的概率是多少?
(2)小明先从左端 $ A $,$ B $,$ C $ 三个绳头中随机选两个打一个结,再从右端 $ A_{1} $,$ B_{1} $,$ C_{1} $ 三个绳头中随机选两个打一个结,求这三根绳子能连接成一根长绳的概率。

答案:
解:
(1)P(选中$AA_1$)=$\frac{1}{3}$.
(2)列表如下:
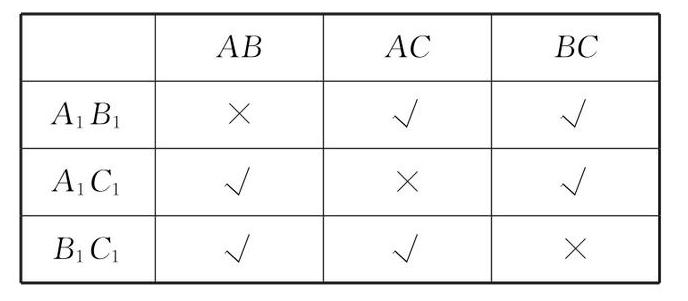
所有等可能的情况有9种,其中这三根绳子能连接成一根长绳的情况有6种,则P(能连接成一根长绳)=$\frac{6}{9}$=$\frac{2}{3}$.
解:
(1)P(选中$AA_1$)=$\frac{1}{3}$.
(2)列表如下:

所有等可能的情况有9种,其中这三根绳子能连接成一根长绳的情况有6种,则P(能连接成一根长绳)=$\frac{6}{9}$=$\frac{2}{3}$.
11. 材料阅读:
骰子是中国古代民间娱乐用来投掷的博具,相传是三国时期魏国曹植所造。近年来,除了普通骰子,还出现了“正四面体骰子”。
如图①,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字 $ 1 $,$ 2 $,$ 3 $,$ 4 $。
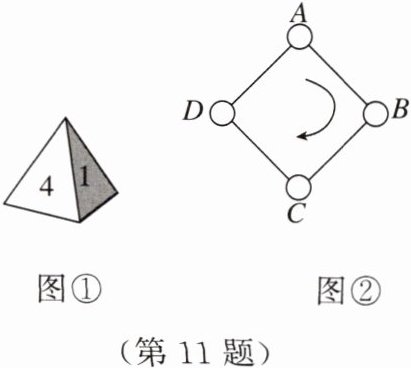
如图②,正方形 $ ABCD $ 的四个顶点处各有一个圈。跳圈游戏的规则:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长。
如:若从圈 $ A $ 起跳,第一次掷得 $ 3 $,就顺时针连续跳 $ 3 $ 个边长,落到圈 $ D $;若第二次掷得 $ 2 $,就从圈 $ D $ 开始顺时针连续跳 $ 2 $ 个边长,落到圈 $ B … … $
设游戏者从圈 $ A $ 起跳。
(1)嘉嘉随机掷一次骰子,求落回到圈 $ A $ 的概率 $ P_{1} $。
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈 $ A $ 的概率 $ P_{2} $,她与嘉嘉落回到圈 $ A $ 的可能性一样吗?
骰子是中国古代民间娱乐用来投掷的博具,相传是三国时期魏国曹植所造。近年来,除了普通骰子,还出现了“正四面体骰子”。
如图①,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字 $ 1 $,$ 2 $,$ 3 $,$ 4 $。

如图②,正方形 $ ABCD $ 的四个顶点处各有一个圈。跳圈游戏的规则:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长。
如:若从圈 $ A $ 起跳,第一次掷得 $ 3 $,就顺时针连续跳 $ 3 $ 个边长,落到圈 $ D $;若第二次掷得 $ 2 $,就从圈 $ D $ 开始顺时针连续跳 $ 2 $ 个边长,落到圈 $ B … … $
设游戏者从圈 $ A $ 起跳。
(1)嘉嘉随机掷一次骰子,求落回到圈 $ A $ 的概率 $ P_{1} $。
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈 $ A $ 的概率 $ P_{2} $,她与嘉嘉落回到圈 $ A $ 的可能性一样吗?
答案:
解:
(1)$p_1$=$\frac{1}{4}$.
(2)列表如下:
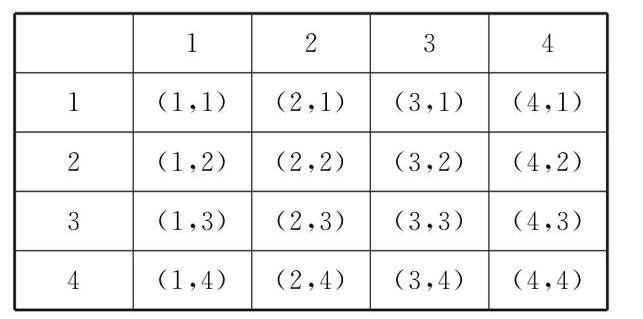
所有等可能的结果共有16种,当两次掷得的数字和为4的倍数,即(1,3),(2,2),(3,1),(4,4)时,才可落回到圈A,共4种,
$\therefore p_2$=$\frac{4}{16}$=$\frac{1}{4}$,
$\therefore$淇淇与嘉嘉落回到圈A的可能性一样.
解:
(1)$p_1$=$\frac{1}{4}$.
(2)列表如下:

所有等可能的结果共有16种,当两次掷得的数字和为4的倍数,即(1,3),(2,2),(3,1),(4,4)时,才可落回到圈A,共4种,
$\therefore p_2$=$\frac{4}{16}$=$\frac{1}{4}$,
$\therefore$淇淇与嘉嘉落回到圈A的可能性一样.
查看更多完整答案,请扫码查看


