第88页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
2. 如图,将一块三角形木板截去一部分后,剩余木板的周长比原来木板的周长长。得到这个结论的依据是(
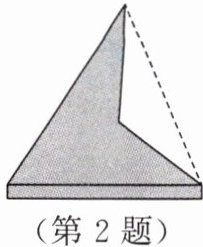
A.两直线相交只有一个交点
B.两点确定一条直线
C.经过一点有无数条直线
D.两点之间,线段最短
D
)。
A.两直线相交只有一个交点
B.两点确定一条直线
C.经过一点有无数条直线
D.两点之间,线段最短
答案:
D
3. 在 $8:30$ 这一时刻,钟面上时针和分针之间夹角的度数为(
A.$85^{\circ}$
B.$75^{\circ}$
C.$70^{\circ}$
D.$60^{\circ}$
B
)。A.$85^{\circ}$
B.$75^{\circ}$
C.$70^{\circ}$
D.$60^{\circ}$
答案:
B
4. 下列单位换算结果不正确的是(
A.$0.25^{\circ} = 900''$
B.$1.5^{\circ} = 90'$
C.$1000'' = (\frac{5}{18})^{\circ}$
D.$125.45^{\circ} = 125^{\circ}24'$
D
)。A.$0.25^{\circ} = 900''$
B.$1.5^{\circ} = 90'$
C.$1000'' = (\frac{5}{18})^{\circ}$
D.$125.45^{\circ} = 125^{\circ}24'$
答案:
D
5. 如图,线段 $AB$ 上有 $C$,$D$,$E$ 三个点,$AC = CD = DE = EB$,下列结论不正确的是(
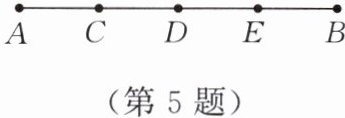
A.$C$ 是线段 $AD$ 的中点
B.$CE = \frac{1}{2}AB$
C.$E$ 既是线段 $DB$ 的中点,又是线段 $CB$ 的中点
D.$D$ 既是线段 $AB$ 的中点,又是线段 $CE$ 的中点
C
)。
A.$C$ 是线段 $AD$ 的中点
B.$CE = \frac{1}{2}AB$
C.$E$ 既是线段 $DB$ 的中点,又是线段 $CB$ 的中点
D.$D$ 既是线段 $AB$ 的中点,又是线段 $CE$ 的中点
答案:
C
6. 一个多边形从一个顶点最多可以引出 12 条对角线,这些对角线把这个多边形分成的三角形的个数是(
A.11
B.12
C.13
D.14
C
)。A.11
B.12
C.13
D.14
答案:
C
7. 【综合与实践】七巧板起源于我国宋代,后流传于世界各国。在综合与实践课堂上,数学兴趣小组同学用一张边长为 $4\mathrm{cm}$ 的正方形纸板依据图①,经过折叠、剪贴,制作了如图②所示的七巧板,再拼成选项中所示的作品——奔跑。其中阴影部分面积为 $5\mathrm{cm}^2$ 的是(
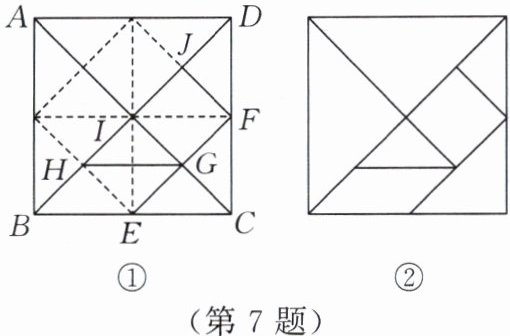
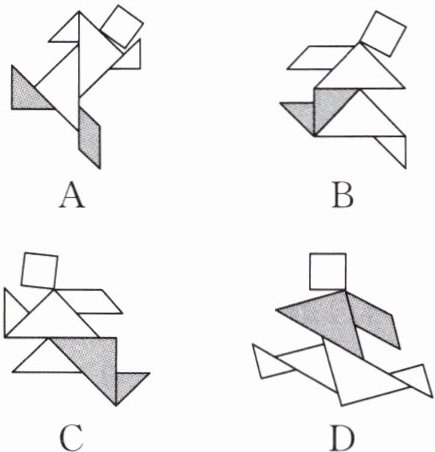
C
)。

答案:
C
8. 【数学应用】王大爷去登山时携带了一根登山杖。如图①,这款可伸缩登山杖共有三节,我们把登山杖的三节类似看成三条线段,其中上节 $EF$ 是固定不动的,长为 $54\mathrm{cm}$,它比中节 $CD$ 长 $7\mathrm{cm}$,中节 $CD$ 又比下节 $AB$ 长 $3\mathrm{cm}$。如图②,在无伸缩的初始状态下,点 $D$,$E$ 重合,点 $B$,$C$ 也是重合的。
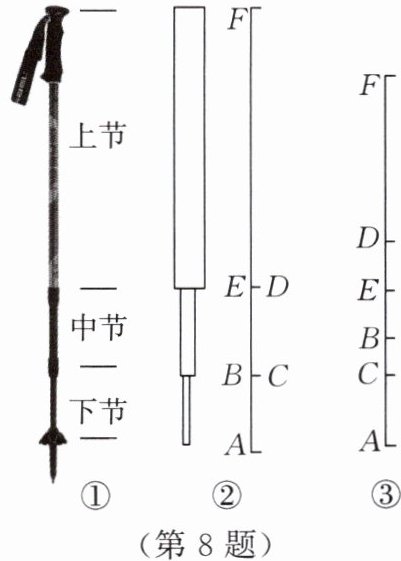
(1)在无伸缩的初始状态下,求登山杖 $AF$ 的长;
(2)如图③,在登山过程中,需要根据不同地形调整登山杖的长度,当总长度 $AF$ 缩短为 $116\mathrm{cm}$ 时,点 $C$ 恰为 $AE$ 的中点,分别求缩进部分 $BC$ 和 $DE$ 的长。

(1)在无伸缩的初始状态下,求登山杖 $AF$ 的长;
(2)如图③,在登山过程中,需要根据不同地形调整登山杖的长度,当总长度 $AF$ 缩短为 $116\mathrm{cm}$ 时,点 $C$ 恰为 $AE$ 的中点,分别求缩进部分 $BC$ 和 $DE$ 的长。
答案:
解:
(1)因为上节EF是固定的,长为54 cm,它比中节CD长7 cm,所以EF=54 cm,CD=54 - 7=47(cm)。因为中节CD比下节AB长3 cm,所以AB=47 - 3=44(cm)。因为AF=EF+CD+AB=54+47+44=145(cm)。所以无伸缩的初始状态下,登山杖AF的长为145 cm。
(2)因为AF=116 cm,EF=54 cm,所以AE=AF - EF=116 - 54=62(cm)。因为点C是AE的中点,所以AC=CE= $\frac{1}{2}$AE=31(cm)。因为AB=44 cm,所以BC=AB - AC=44 - 31=13(cm)。因为CD=47 cm,所以DE=CD - CE=47 - 31=16(cm)。所以缩进部分BC的长为13 cm,DE的长为16 cm。
(1)因为上节EF是固定的,长为54 cm,它比中节CD长7 cm,所以EF=54 cm,CD=54 - 7=47(cm)。因为中节CD比下节AB长3 cm,所以AB=47 - 3=44(cm)。因为AF=EF+CD+AB=54+47+44=145(cm)。所以无伸缩的初始状态下,登山杖AF的长为145 cm。
(2)因为AF=116 cm,EF=54 cm,所以AE=AF - EF=116 - 54=62(cm)。因为点C是AE的中点,所以AC=CE= $\frac{1}{2}$AE=31(cm)。因为AB=44 cm,所以BC=AB - AC=44 - 31=13(cm)。因为CD=47 cm,所以DE=CD - CE=47 - 31=16(cm)。所以缩进部分BC的长为13 cm,DE的长为16 cm。
查看更多完整答案,请扫码查看


