《2025年伴你学北京师范大学出版社七年级数学上册北师大版山西专版》

3. $-2.5$ 不是(B)。

A.负数
B.整数
C.有理数
D.分数

答案： B

4. 下列各组量中具有相反意义的量的是(B)。
A.某同学在操场上慢跑 $500m$ 后,加速跑了 $200m$
B.某超市上周亏损 $3000$ 元,本周盈利 $12000$ 元
C.学生甲比学生乙高 $1.5cm$,学生乙比学生甲轻 $2.4kg$
D.小明期中数学成绩为 $50$ 分,期末数学成绩为 $70$ 分

答案： B

5. 下列说法正确的是(B)。
A.一个有理数不是正数就是负数
B.整数和分数统称有理数
C.正整数和负整数统称整数
D.最小的整数是 $0$

答案： B

6. 把下列各数填入所属的集合内：
$\frac{22}{7}$,$-2$,$-7.\dot{6}\dot{5}$,$0$,$-0.1313313331…$(每两个 $1$ 之间依次增加 $1$ 个 $3$),$-21.25$,$7$,$+5.5$。
整数集合：{-2,0,7…}；
非负整数集合：{0,7…}；
负有理数集合：{$-2,-7.\dot{6}\dot{5},-21.25$…}；
正分数集合：{$\frac{22}{7}$,+5.5…}。

答案： 整数集合：{-2,0,7…}；非负整数集合：{0,7…}；负有理数集合：${-2,-7.\dot{6}\dot{5},-21.25…}；$正分数集合：${\frac{22}{7},+5.5…}$

7. 有 $8$ 筐白菜,它们的质量(单位：$kg$)分别为 $25.8$,$26$,$24.2$,$27.2$,$23$,$25$,$22.5$,$24$。请你设定一个标准,用正负数或 $0$ 来表示它们的质量。

答案： 答案不唯一,合理即可。例:设定标准为25 kg,超出部分记为“+”,不足部分记为“-”,这8筐白菜的质量(单位:kg)分别表示为+0.8,+1,-0.8,+2.2,-2,0,-2.5,-1。

8. 【数学应用】如图,一名跳水运动员参加 $10m$ 跳台的跳水比赛($10m$ 跳台是指跳台离水面的高度为 $10m$)。这名运动员的身高为 $1.75m$,水深为 $5.4m$。(规定向上为正)
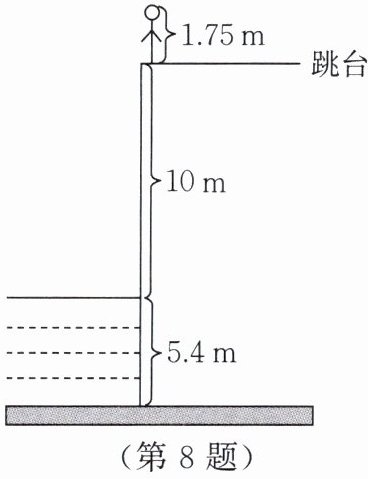
(1) 若以水面为基准,则这名运动员头顶的高度及池底的深度分别如何表示？
(2) 若以跳台为基准,则池底的深度与水面的高度分别如何表示？

答案： 解:
(1)以水面为基准,这名运动员头顶的高度为10+1.75=11.75(m),表示为+11.75 m,池底的深度表示为-5.4 m。
(2)池底距跳台10+5.4=15.4(m),以跳台为基准,池底的深度表示为-15.4 m,水面的高度表示为-10 m。

9. 将$ 1,-\frac{1}{2},\frac{1}{3},-\frac{1}{4},\frac{1}{5},-\frac{1}{6},… $按一定规律排列如下：
第 1 行 1
第 2 行$ -\frac{1}{2},\frac{1}{3}$
第 3 行$ -\frac{1}{4},\frac{1}{5},-\frac{1}{6}$
第 4 行$ \frac{1}{7},-\frac{1}{8},\frac{1}{9},-\frac{1}{10}$
第 5 行$ \frac{1}{11},-\frac{1}{12},\frac{1}{13},-\frac{1}{14},\frac{1}{15}$
…则第 20 行从左到右第 10 个数是$-\frac{1}{200}$。

答案： $-\frac{1}{200}$