《2025年伴你学北京师范大学出版社七年级数学上册北师大版山西专版》

1. $-4$的倒数是(B)。

A.$-4$
B.$-\dfrac{1}{4}$
C.$\dfrac{1}{4}$
D.$4$

答案： B

2. $-3^{6}$表示(C)。

A.$6个-3$相乘的积
B.$-3与6$相乘的积
C.$6个3$相乘的积的相反数
D.$6与3$相乘的积

答案： C

3. 用计算器计算$(3.1×105)×(7.6×108)$,按的第$5$个键是(C)。
A.$\textcircled{5}$
B.$\textcircled{0}$
C.$\textcircled{×}$
D.$\textcircled{1}$

答案： C

4. 下列计算结果正确的是(D)。
A.$-6÷\dfrac{2}{3}= 9$
B.$-8÷\left(-\dfrac{2}{3}\right)×\dfrac{1}{2}= 24$
C.$-3^{2}+1= 10$
D.$9×\left(-\dfrac{1}{3}\right)^{3}= -\dfrac{1}{3}$

答案： D

5. 在$-(+2),-3^{2},\left(-\dfrac{1}{3}\right)^{4},-\dfrac{2^{2}}{5},-(-1)^{1023},-|-3|$中,负数共有(C)。
A.$2$个
B.$3$个
C.$4$个
D.$5$个

答案： C

6. 晋阳湖坐落于山西省太原市南端金胜镇内,原为人工开挖的电厂蓄水池,该湖水域面积为$5.1$平方千米,蓄水量达$2400$万立方米,素有“中国北湖”之称。$2400$万用科学记数法表示为2.4×10⁷。

答案： 2.4×10⁷

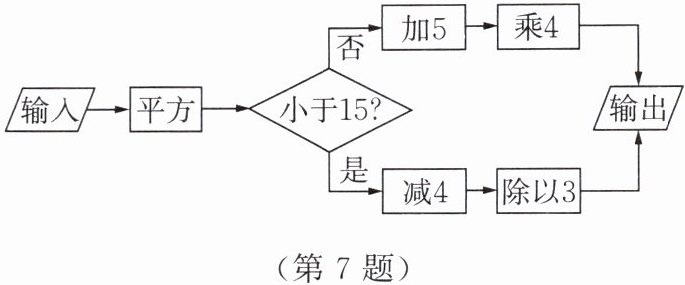
7. 热爱计算机编程的小明编写了如图所示的程序,运行该程序,若输入的值为$-3$,则输出的值为$\frac{5}{3}$。
]

答案： $\frac{5}{3}$

8. 用计算器计算下列各式,将结果写在横线上：
(1)$9×9+19=$100,
$99×99+199=$10000,
$999×999+1999=$1000000,
$9999×9999+19999=$100000000。
(2)仔细观察上述各式,根据你所发现的规律直接写出以下算式的运算结果：
$999999×999999+1999999=$1000000000000。

答案：
(1)100 10 000 1 000 000 100 000 000
(2)1 000 000 000 000

9. 计算：
(1)$\left(-\dfrac{1}{3}+\dfrac{1}{4}\right)×(-24)-7$；
(2)$-(-1)+3^{2}÷(-4+1)×2$；
(3)$(-2)^{3}÷(-2.5+2.4)-(-1)^{200}$；
(4)$-3^{6}-6.4×\left(-\dfrac{1}{8}\right)$。

答案：
(1)$(-\frac{1}{3}+\frac{1}{4})×(-24)-7$=$(-\frac{1}{3})×(-24)+\frac{1}{4}×(-24)-7$=8-6-7=-5。
(2)$-(-1)+3^{2}÷(-4+1)×2$=1+9÷(-3)×2=1-6=-5。
(3)$(-2)^{3}÷(-2.5+2.4)-(-1)^{200}$=-8÷(-0.1)-1=80-1=79。
(4)$-3^{6}-6.4×(-\frac{1}{8})$=-729+6.4×$\frac{1}{8}$=-729+0.8=-728.2。