《2025年伴你学北京师范大学出版社七年级数学上册北师大版山西专版》

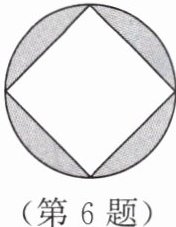
6. 如图,某餐桌桌面可由圆形折叠成正方形(图中阴影表示可折叠部分)。若折叠前圆形桌面的直径为 $ a m $,折叠成正方形后其边长为 $ b m $,则桌面可折叠部分的面积为$\frac{\pi}{4}a^{2}-b^{2}$。(用含 $ a $,$ b $ 的代数式表示,保留 $ \pi $)

答案： $\frac{\pi}{4}a^{2}-b^{2}$

7. 先化简,再求值：
(1) $ 6xy - 3x^{2}y + xy - 2x^{2}y + 3 $,其中 $ x= -2 $,$ y= -3 $；
(2) $ 5ab^{2}-[2a^{2}b-(4ab^{2}-2a^{2}b)] $,其中 $ |a - 2|+(b + 1)^{2}= 0 $。

答案：
(1)6xy-3x²y+xy-2x²y+3=7xy-5x²y+3。当x=-2,y=-3时,原式=7xy-5x²y+3=7×(-2)×(-3)-5×(-2)²×(-3)+3=42+60+3=105。
(2)5ab²-[2a²b-(4ab²-2a²b)]=9ab²-4a²b。当|a-2|+(b+1)²=0时,a=2,b=-1,所以原式=9ab²-4a²b=9×2×(-1)²-4×2²×(-1)=34。

8. 对多项式 $ x - y - z - m - n $ 任意加括号后仍然只含减法运算并将所得式子化简,称为“加算操作”,例如 $ (x - y)-(z - m - n)= x - y - z + m + n $,$ x - y-(z - m)-n= x - y - z + m - n $ 等,有下列说法：
① 至少存在一种“加算操作”,使其结果与原多项式相等；
② 不存在任何“加算操作”,使其结果与原多项式之和为 $ 0 $；
③ 所有的“加算操作”共有 $ 8 $ 种不同的结果。
其中正确的说法有(D)。
A.$ 0 $ 个
B.$ 1 $ 个
C.$ 2 $ 个
D.$ 3 $ 个

答案： D

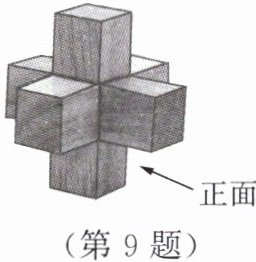
9. 【数学文化】鲁班锁是中国传统的智力玩具,起源于中国古代建筑中首创的榫卯结构,十分巧妙。如图所示的是一种简单的鲁班锁,由三根完全相同的四棱柱木条,挖去中间部分,使其内部凹凸啮合,组成外观严丝合缝的十字形几何体,其上下、左右、前后分别对称。已知这些四棱柱木条的高为 $ 3a $,底面正方形的边长为 $ a $,则这个鲁班锁的表面积为______30a²。(用含 $ a $ 的代数式表示)

答案： 30a²