第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
5. 某奶茶店上周的盈亏情况(盈余记为正,亏损记为负,单位:元)如下:+500,-1000,-1030,+1250,-870,+350,+980,则上周的盈亏情况是(
A.盈余
B.亏损
C.不盈不亏
D.无法判断
A
)。A.盈余
B.亏损
C.不盈不亏
D.无法判断
答案:
A
6. 【数学应用】下图是陈阿姨手机里某支付平台连续四笔的交易记录,已知在此之前该支付账户的余额为 1470 元,则这四笔交易后,她支付账户的余额为(
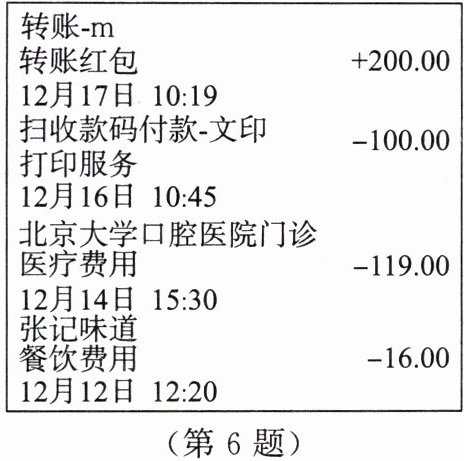
A.1405 元
B.1425 元
C.1415 元
D.1435 元
D
)。
A.1405 元
B.1425 元
C.1415 元
D.1435 元
答案:
D
7. 【链接教材】下表为今年雨季某防汛小组测量的某条河流一星期的水位变化情况:
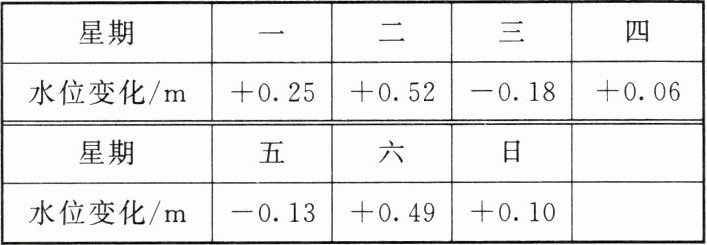
(注:正号表示比前一天水位上升,负号表示比前一天水位下降)
(1)若本周日达到了警戒水位 73.4 m,则本周一的水位是多少?上周日的水位是多少?
(2)在(1)的条件下,本周哪一天河流水位最高?哪一天水位最低?它们位于警戒水位之上还是之下?
(3)与上周日相比,本周日的河流水位是上升了还是下降了?

(注:正号表示比前一天水位上升,负号表示比前一天水位下降)
(1)若本周日达到了警戒水位 73.4 m,则本周一的水位是多少?上周日的水位是多少?
(2)在(1)的条件下,本周哪一天河流水位最高?哪一天水位最低?它们位于警戒水位之上还是之下?
(3)与上周日相比,本周日的河流水位是上升了还是下降了?
答案:
解:
(1)本周一的水位是72.54 m,上周日的水位是72.29 m。
(2)本周日河流水位最高;本周一水位最低;本周日位于警戒水位,本周一位于警戒水位之下。
(3)与上周日相比,本周日的河流水位上升了。
(1)本周一的水位是72.54 m,上周日的水位是72.29 m。
(2)本周日河流水位最高;本周一水位最低;本周日位于警戒水位,本周一位于警戒水位之下。
(3)与上周日相比,本周日的河流水位上升了。
8. 观察下列两组等式:① $\frac{1}{1×2}= 1-\frac{1}{2}$,$\frac{1}{2×3}= \frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}= \frac{1}{3}-\frac{1}{4}$,…;
② $\frac{1}{1×4}= \frac{1}{3}×(1-\frac{1}{4})$,$\frac{1}{4×7}= \frac{1}{3}×(\frac{1}{4}-\frac{1}{7})$,$\frac{1}{7×10}= \frac{1}{3}×(\frac{1}{7}-\frac{1}{10})$,…。
计算:(1) $\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+\frac{1}{4×5}$;
(2) $\frac{1}{1×6}+\frac{1}{6×11}+\frac{1}{11×16}+…+\frac{1}{51×56}$。
② $\frac{1}{1×4}= \frac{1}{3}×(1-\frac{1}{4})$,$\frac{1}{4×7}= \frac{1}{3}×(\frac{1}{4}-\frac{1}{7})$,$\frac{1}{7×10}= \frac{1}{3}×(\frac{1}{7}-\frac{1}{10})$,…。
计算:(1) $\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+\frac{1}{4×5}$;
(2) $\frac{1}{1×6}+\frac{1}{6×11}+\frac{1}{11×16}+…+\frac{1}{51×56}$。
答案:
解:
(1)$\frac{1}{1× 2}+\frac{1}{2× 3}+\frac{1}{3× 4}+\frac{1}{4× 5}$
$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}$
$=1-\frac{1}{5}$
$=\frac{4}{5}$。
(2)$\frac{1}{1× 6}+\frac{1}{6× 11}+\frac{1}{11× 16}+\cdots +\frac{1}{51× 56}$
$=\frac{1}{5}× \left(1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+\frac{1}{11}-\frac{1}{16}+\cdots +\frac{1}{51}-\frac{1}{56}\right)$
$=\frac{1}{5}× \left(1-\frac{1}{56}\right)$
$=\frac{1}{5}× \frac{55}{56}$
$=\frac{11}{56}$。
(1)$\frac{1}{1× 2}+\frac{1}{2× 3}+\frac{1}{3× 4}+\frac{1}{4× 5}$
$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}$
$=1-\frac{1}{5}$
$=\frac{4}{5}$。
(2)$\frac{1}{1× 6}+\frac{1}{6× 11}+\frac{1}{11× 16}+\cdots +\frac{1}{51× 56}$
$=\frac{1}{5}× \left(1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+\frac{1}{11}-\frac{1}{16}+\cdots +\frac{1}{51}-\frac{1}{56}\right)$
$=\frac{1}{5}× \left(1-\frac{1}{56}\right)$
$=\frac{1}{5}× \frac{55}{56}$
$=\frac{11}{56}$。
查看更多完整答案,请扫码查看


