《2025年新坐标同步练习九年级数学上册人教版青海专用》

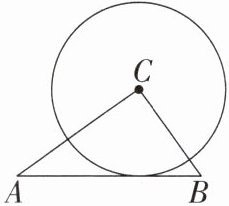
10. 如图,在$\triangle ABC$中,$AB = 5$,$BC = 3$,$AC = 4$,以点$C为圆心的圆与AB$相切,则$\odot C$的半径为(B)

A.$2.3$
B.$2.4$
C.$2.5$
D.$2.6$

答案： B

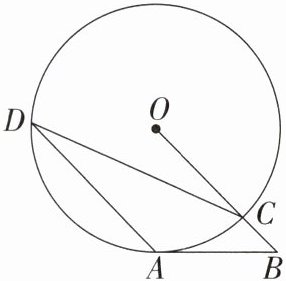
11. 如图,在$\odot O$中,$AB切\odot O于点A$,连接$OB交\odot O于点C$,过点$A作AD// OB交\odot O于点D$,连接$CD$. 若$\angle B = 46^{\circ}$,则$\angle OCD$的度数为(A)

A.$22^{\circ}$
B.$23^{\circ}$
C.$24^{\circ}$
D.$25^{\circ}$

答案： A

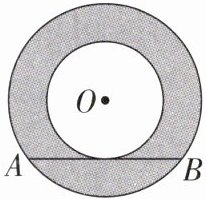
12. 如图,两圆圆心相同,大圆的弦$AB$与小圆相切,$AB = 8$,则图中阴影部分的面积是16π(结果保留$\pi$).

答案： 解析:设AB与小圆的切点为C,连接OC,OB(图略).因为AB与小圆相切于点C,所以OC⊥AB,所以BC= $\frac{1}{2}$AB=4,所以 $S_{阴影}=π(OB^{2}-OC^{2})=π\cdot BC^{2}=16π$.答案:16π

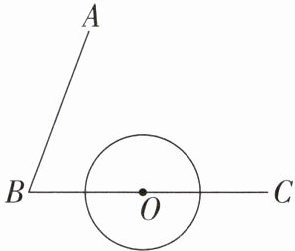
13. 如图,$\angle ABC = 70^{\circ}$,$O为射线BC$上一点,以点$O$为圆心,$\frac{1}{2}OB$长为半径作圆. 将射线$BA绕点B$顺时针旋转,使射线$BA与\odot O$相切,则旋转角的度数是40°或100°.

答案： 40°或100°

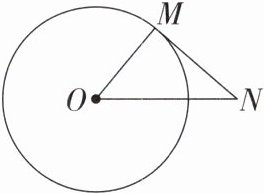
14. (2023·青海)如图,$MN是\odot O$的切线,$M$是切点,连接$OM$,$ON$. 若$\angle N = 37^{\circ}$,则$\angle MON$的度数是53°.

答案： 解析:因为MN是⊙O的切线,M是切点,所以∠OMN=90°.又因为∠N=37°,所以∠MON=90°-∠N=53°.答案:53°

15. (2024·临夏)如图,直线$l与\odot O相切于点D$,$AB为\odot O$的直径,过点$A作AE\perp l于点E$,延长$AB交直线l于点C$.

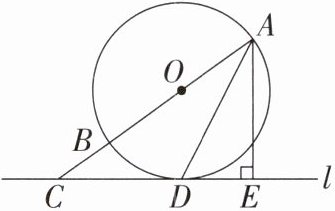
(1)求证：$AD平分\angle CAE$；
(2)如果$BC = 1$,$DC = 3$,求$\odot O$的半径.

答案：
(1)证明:如图,连接OD. 因为直线l与⊙O相切于点D,所以OD⊥l.又因为AE⊥l,所以OD//AE,所以∠DAE=∠ADO.因为OA=OD,所以∠DAO=∠ADO,所以∠DAO=∠DAE,即AD平分∠CAE.
(2)设⊙O的半径为r,则OC=OB+BC=r+1,OD=r.在Rt△OCD中,$OD^{2}+CD^{2}=OC^{2}$,所以 $r^{2}+3^{2}=(r+1)^{2}$,解得r=4,所以⊙O的半径为4.