《2025年新坐标同步练习九年级数学上册人教版青海专用》

2.某商品每件进价为20元,销售期间发现,当售价为25元时,每天可售出120件,销售单价每降价1元,每天销售量增加10件.现商家决定降价销售,每件降价$x$元($0＜x＜5$).设每天销售量为$y$件,每天销售商品获得的利润为$w$元,则下列函数关系式正确的是 (C)
A.$y = 10x - 120$
B.$y = -10x + 120$
C.$w = (10x + 120)(25 - 20 - x)$
D.$w = (-10x + 120)(25 - 20 - x)$

答案： C

3.一件工艺品进价为100元,按标价135元售出,每天可售出100件.根据销售统计,一件工艺

品

每

降价1元出售,则每天可多售出4件,要使每天获得的利润最大,每件需降价 (B)

A.4元
B.5元
C.8元
D.10元

答案： B

4.某民俗旅游村因游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出.若每张床位每天收费提高20元,则相应地减少了10张床位的租出.如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是(C)
A.140元
B.150元
C.160元
D.180元

答案： 解析:选 C.设每张床位每天收费 x 元,总租金为 y 元,则$y=x\left(100-\frac{x-100}{20}× 10\right)=-\frac{1}{2}x^{2}+150x=-\frac{1}{2}(x-150)^{2}+11250$,所以此抛物线的对称轴为$x=150$,又因为每张床位每天以 20 元为单位提高收费,又为使租出的床位少且租金高,所以每张床位每天最合适的收费是 160 元.

5.某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,售价每涨价1元,月销售量就减少10千克,则月销售利润$y$(单位:元)与售价$x$(单位:元/千克)之间的函数解析式为（$y=-10x²+1400x-40000$）

答案： 解析:由题意可得,y=(x-40)[500-10(x-50)]=-10x²+1400x-40000,即月销售利润 y(单位:元)与售价 x(单位:元/千克)之间的函数解析式是$y=-10x²+1400x-40000$.答案:$y=-10x²+1400x-40000$

6.某电商以每件40元的价格购进某款T恤,以每件60元的价格出售.经统计,“十一”的前一周每天的销售量为500件,该电商在“十一黄金周”期间进行降价销售.经调查,发现该T恤在“十一”前一周销售量的基础上,每降价1元,“十一黄金周”期间每天的销售量就会增加50件.若要求销售单价不低于进价,且按照物价部门规定销售利润率不高于$30\%$,那么当该电商获得最大利润时,每件T恤的售价为 （52）元.

答案： 解析:设销售单价为 x 元,获得的利润为 w 元,则降价(60-x)元,每件盈利(x-40)元,每天可售出[500+50(60-x)]=(-50x+3500)件.根据题意,得w=(x-40)(-50x+3500)=-50x²+5500x-140000=-50(x-55)²+11250.因为-50＜0,所以抛物线开口向下,函数有最大值,且距离对称轴越远的函数值越小.因为要求销售单价不低于进价,且按照物价部门规定销售利润率不高于30%,即售价不能超过30%×40+40=52(元),所以40≤x≤52,所以当x=52时,w取得最大值.答案:52

7.某超市对进货价为10元/千克的某品种苹果的销售情况进行统计,发现每天销售量$y$(千克)与销售单价$x$(元/千克)之间存在一次函数关系,如图.

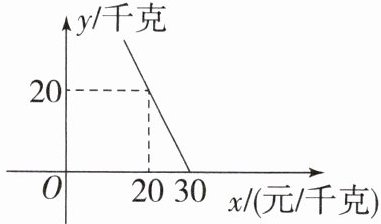
(1)求$y与x$之间的函数关系式(不要求写出$x$的取值范围)；
(2)应怎样确定销售单价,才能使该品种苹果每天的销售利润最大？最大利润是多少？

答案： 解:
(1)设$y=kx+b$,将(20,20),(30,0)代入,得$\left\{\begin{array}{l} 20k+b=20,\\ 30k+b=0,\end{array}\right.$解得$\left\{\begin{array}{l} k=-2,\\ b=60.\end{array}\right.$所以 y 与 x 之间的函数关系式是$y=-2x+60$.
(2)设每天的销售利润为 w 元,则$w=(x-10)y=(x-10)(-2x+60)=-2x²+80x-600=-2(x-20)²+200$.所以当x=20时,w取得最大值.所以当销售单价定为20元/千克时,该品种苹果每天的销售利润最大,最大利润是200元.