《2025年新坐标同步练习九年级数学上册人教版青海专用》

9. 若抛物线 $ y = 2x^{m^{2}-4m - 3}+(m - 5) $ 的顶点在 $ x $ 轴下方,则 $ m $ 的值为 (B)
A.$ m = 5 $
B.$ m = - 1 $
C.$ m = 5 $ 或 $ m = - 1 $
D.$ m = - 5 $

答案： 解析:选B.因为$y=2x^{m^{2}-4m-3}+(m-5)$的图象是抛物线,所以$m^{2}-4m-3=2$,解得$m=5$或-1.又因为抛物线的顶点坐标是$(0,m-5)$,顶点在x轴下方,所以$m-5＜0$,即$m＜5$,所以$m=-1$.故选B.

10. 下列关于二次函数 $ y = 3x^{2} - 1 $ 的图象的说法,错误的是 (B)
A.它的对称轴是直线 $ x = 0 $
B.在对称轴的左侧,$ y $ 随 $ x $ 的增大而增大
C.它的顶点坐标是$(0,-1)$
D.它的图象有最低点

答案： B

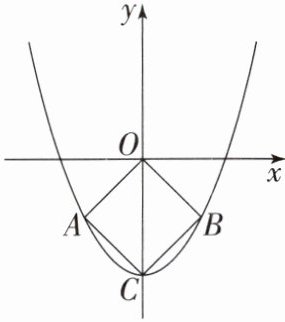
11. 如图,抛物线 $ y = ax^{2} - c $ 经过正方形 $ OACB $ 的三个顶点 $ A,B,C $,点 $ C $ 在 $ y $ 轴上,则 $ ac $ 的值为( )


A.1
B.2
C.3
D.4

答案：
解析:选B.连接AB,交y轴于点D.
　　　　　　　
当$x=0$时,则$y=-c$,即$OC=c$.因为四边形OACB是正方形,所以$AB=OC=2AD=2OD=c$,$AD⊥OD$,所以点$A(-\frac {c}{2},-\frac {c}{2})$,所以$-\frac {c}{2}=a×(-\frac {c}{2})^{2}-c$,解得$ac=2$.故选B.

12. 已知抛物线 $ y = ax^{2} + c $ 与 $ y = 2x^{2} $ 的形状相同,开口方向相反,且经过点$(-1,5)$,则其解析式为$y=-2x^{2}+7$.

答案： $y=-2x^{2}+7$

13. 已知二次函数 $ y = (m - 1)x^{2} + m^{2} + 1 $ 有最大值 5,则 $ m = $-2.

答案： -2

14. 已知 $ A(-2,y_{1}),B(5,y_{2}) $ 为函数 $ y = x^{2} + a $ 图象上的两点,比较 $ y_{1} $ 与 $ y_{2} $ 的大小：$ y_{1} $＜$ y_{2} $(选填“$ ＞ $”“$ ＜ $”或“$ = $”).

答案： ＜

15. (2024·平凉九年级期中) 我们一般会通过列表、描点、连线的方式来画函数图象,并结合图象研究函数的性质. 请按要求完成对二次函数 $ y = x^{2} - 1 $ 的研究.
(1) 列表：

其中,$ m = $____.
根据表中数据,在如图所示的平面直角坐标系中画出二次函数 $ y = x^{2} - 1 $ 的图象.

(2) 根据函数图象,下列关于该函数性质的说法正确的是____ (填序号).
① 该函数图象是轴对称图形,它的对称轴是 $ y $ 轴；
② 该函数有最小值,没有最大值；
③ 当 $ x ＜ 0 $ 时,$ y $ 随 $ x $ 的增大而增大；当 $ x ＞ 0 $ 时,$ y $ 随 $ x $ 的增大而减小；
④ 当 $ y = 0 $ 时,$ x $ 的值为 1.

答案：

(1)当$x=0$时,$y=x^{2}-1=-1$,所以$m=-1$.故答案为:-1
画出函数的图象如图:
　　　　　
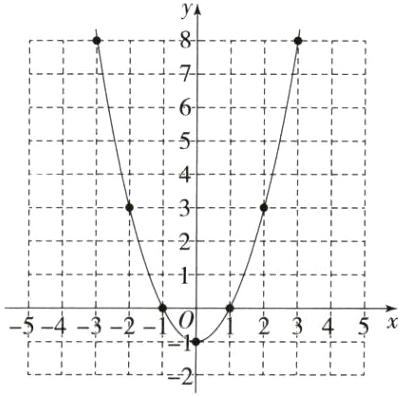
(2)观察图象,①该函数图象是轴对称图形,它的对称轴是y轴.正确;②该函数有最小值,没有最大值.正确;③当$x＜0$时,y随x的增大而减小;当$x＞0$时,y随x的增大而增大.原说法错误;④当$y=0$时,x的值为1或-1.原说法错误.故答案为:①②