《2025年新坐标同步练习九年级数学上册人教版青海专用》

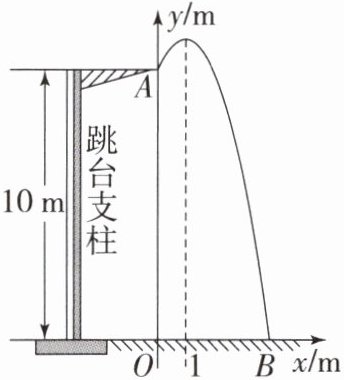
12. 一名运动员在$10m$高的跳台进行跳水,身体(看成一点)在空中的运动轨迹是一条抛物线,运动员离水面$OB的高度y$($m$)与离起跳点$A的水平距离x$($m$)之间的函数关系如图所示,运动员离起跳点$A的水平距离为1m$时达到最高点,当运动员离起跳点$A的水平距离为3m时离水面的距离为7m$.
(1)求$y关于x$的函数表达式；
(2)求运动员从起跳点到入水点的水平距离$OB$的长.

答案：
(1)由题意得，抛物线的对称轴为$x = 1$，经过点$(0,10)$，$(3,7)$，设抛物线的表达式为$y = ax^{2}+bx + c$，所以$\begin{cases}-\frac{b}{2a}=1 \\c = 10 \\9a + 3b + c = 7\end{cases}$，解得$\begin{cases}a = -1 \\b = 2 \\c = 10\end{cases}$，所以$y$关于$x$的函数表达式为$y = -x^{2}+2x + 10$.
(2)令$y = 0$，则$-x^{2}+2x + 10 = 0$，解得$x = 1 + \sqrt{11}$(负值已舍去)，所以运动员从起跳点到入水点的水平距离OB的长为$(1 + \sqrt{11})m$.

13. (2024·兰州改编)在校园科技节期间,科普员为同学们进行了某型号水火箭的发射表演,水火箭发射后的运动路线可以看作是一条抛物线.为了解水火箭的相关性能,同学们进一步展开研究.如图,建立直角坐标系,水火箭发射后落在水平地面$A$处.科普员提供了该型号水火箭与地面成一定角度时,从发射到着陆过程中,水火箭距离地面$OA的竖直高度y$($m$)与离发射点$O的水平距离x$($m$)的几组关系数据如下.



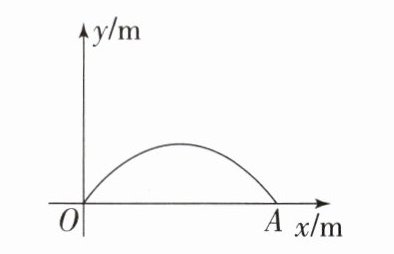
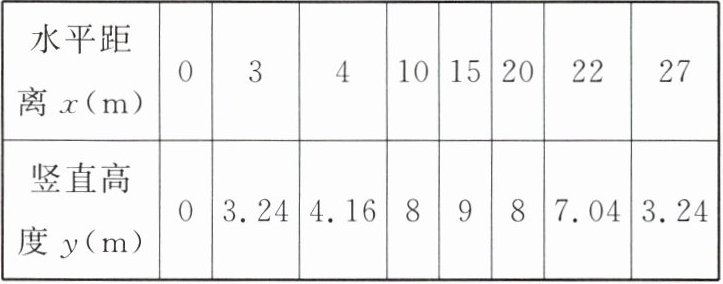
(1)根据上表,请确定抛物线的表达式；
(2)请计算当水火箭飞行至离发射点$O的水平距离为5m$时,水火箭距离地面的竖直高度.

答案：
(1)根据题意可知抛物线过原点，设抛物线的表达式为$y = ax^{2}+bx(a \neq 0)$.由表格得，抛物线的顶点坐标为$(15,9)$，则$\begin{cases}-\frac{b}{2a}=15 \\-\frac{b^{2}}{4a}=9\end{cases}$，解得$\begin{cases}a = -\frac{1}{25} \\b = \frac{6}{5}\end{cases}$，则抛物线的表达式为$y = -\frac{1}{25}x^{2}+\frac{6}{5}x$.
(2)当$x = 5$时，$y = -\frac{1}{25}×5^{2}+\frac{6}{5}×5 = 5$，即水火箭距离地面的竖直高度为5m.