《2025年新坐标同步练习九年级数学上册人教版青海专用》

1. 把实际问题中变量之间的关系用二次函数模型来刻画,利用二次函数的图象和性质来解决实际问题.

答案： 二次函数 图象和性质

2. 如图是一个迷宫游戏盘的局部平面简化示意图,该矩形的长、宽分别为 5 cm、3 cm,其中阴影部分为迷宫中的挡板,设挡板的宽度为 $ x $ cm,小球滚动的区域(空白区域)的面积为 $ y $ $ cm^{2} $,则下列所列方程正确的是(B)

A.$ y = 5×3 - 3x - 5x $
B.$ y = (5 - x)(3 - x) $
C.$ y = 3x + 5x $
D.$ y = (5 - x)(3 - x) + 5x^{2} $

答案： B

3. 用总长为 40 cm 的绳子围成一个矩形,则矩形面积 $ y $($ cm^{2} $)与一边长 $ x $(cm)之间的函数关系式为(C)
A.$ y = x^{2} $
B.$ y = -x^{2} + 40x $
C.$ y = -x^{2} + 20x $
D.$ y = -x^{2} + 20 $

答案： C

4. 用长为 8 m 的铝合金条制成如图形状的矩形窗框,要使窗户的透光面积最大,那么这个窗户的最大透光面积是(C)

A.$ \frac{64}{25} $ $ m^{2} $
B.$ \frac{4}{3} $ $ m^{2} $
C.$ \frac{8}{3} $ $ m^{2} $
D.4 $ m^{2} $

答案： C

5. 用长度一定的绳子围成一个矩形,如果矩形的一边长 $ x $(m)与面积 $ y $($ m^{2} $)满足函数关系 $ y = -(x - 12)^{2} + 144 $($ 0 ＜ x ＜ 24 $),则该矩形面积的最大值为144 $ m^{2} $.

答案： 144

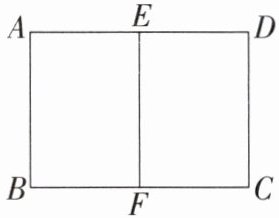
6. 如图,一块矩形土地 $ ABCD $ 由篱笆围着,并且由一条与 $ CD $ 边平行的篱笆 $ EF $ 分开. 已知篱笆的总长为 900 m(篱笆的厚度忽略不计),当 $ AB = $150m 时,矩形土地 $ ABCD $ 的面积最大.

答案： 150

7. 如图,某中学综合与实践小组要围成一个矩形菜园 $ ABCD $,其中一边 $ AD $ 靠墙(墙足够长),其余的三边 $ AB $,$ BC $,$ CD $ 用总长为 40 米的栅栏围成. 设矩形 $ ABCD $ 的边 $ AB = x $ 米,面积为 $ S $ 平方米.

(1)菜园 $ ABCD $ 的面积 $ S $ 与 $ x $ 之间的关系式为S= -2x²+40x(0＜x＜20)；
(2)菜园 $ ABCD $ 的最大面积是200平方米.

答案：
(1)S= -2x²+40x(0＜x＜20)
(2)200

8. 如图,小亮父亲想用长 80 m 的栅栏,再借助房屋的外墙围成一个矩形的羊圈,已知房屋外墙长 50 m,设矩形 $ ABCD $ 的边 $ AB = x $ m,面积为 $ S $ $ m^{2} $.

(1)写出 $ S $ 与 $ x $ 之间的函数关系式,并写出 $ x $ 的取值范围；
(2)当 $ AB $,$ BC $ 分别为多少米时,羊圈的面积最大？最大值是多少？

答案： 解:
(1)因为AB=CD=x m,所以BC=(80-2x)m,所以S=x(80-2x)= -2x²+80x.因为$\begin{cases} AB＞0, \\ 0＜BC\leqslant50, \end{cases}$即$\begin{cases} x＞0, \\ 0＜80-2x\leqslant50, \end{cases}$所以$\begin{cases} x＞0, \\ 15\leqslant x＜40, \end{cases}$所以15≤x＜40,所以S= -2x²+80x(15≤x＜40).
(2)S= -2(x²-40x+400-400)= -2(x-20)²+800,因为15≤x＜40,所以当x=20时,S有最大值为800,所以当AB=20 m,BC=40 m时,羊圈的面积最大,最大值为800 $m^{2}$.