第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
1. 已知下列一组数:$1,\frac {3}{4},\frac {5}{9},\frac {7}{16},\frac {9}{25},... $,用代数式表示第n个数,则第n个数是(
A.$\frac {2n-1}{3n-2}$
B.$\frac {2n-1}{n^{2}}$
C.$\frac {2n+1}{3n-2}$
D.$\frac {2n+1}{n^{2}}$
B
)A.$\frac {2n-1}{3n-2}$
B.$\frac {2n-1}{n^{2}}$
C.$\frac {2n+1}{3n-2}$
D.$\frac {2n+1}{n^{2}}$
答案:
B
2. 如图,填在各方格中的三个数之间均具有相同的规律,根据此规律,n的值是(
A.48
B.56
C.63
D.74
C
)A.48
B.56
C.63
D.74
答案:
C
3. 古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”。如图,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,则下列符合这一规律的等式是(
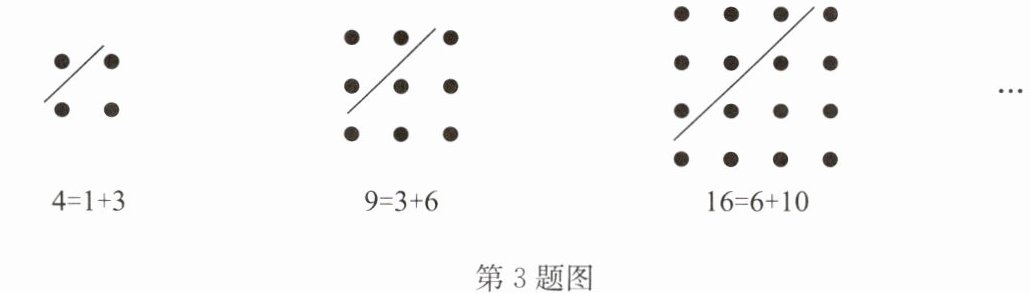
A.$20= 4+16$
B.$25= 9+16$
C.$36= 15+21$
D.$40= 12+28$
C
)
A.$20= 4+16$
B.$25= 9+16$
C.$36= 15+21$
D.$40= 12+28$
答案:
C
4. (2024·梁溪区月考)有一组数据:$a_{1}= \frac {3}{1×2×3},a_{2}= \frac {5}{2×3×4},a_{3}= \frac {7}{3×4×5},...,a_{n}= \frac {2n+1}{n(n+1)(n+2)}$。 记$S_{n}= a_{1}+a_{2}+a_{3}+... +a_{n}$,则$S_{12}=$(
记$S_{n}= a_{1}+a_{2}+a_{3}+... +a_{n}$,则$S_{12}=$(
A.$\frac {201}{182}$
B.$\frac {203}{180}$
C.$\frac {199}{198}$
D.$\frac {203}{184}$
 记$S_{n}= a_{1}+a_{2}+a_{3}+... +a_{n}$,则$S_{12}=$(
记$S_{n}= a_{1}+a_{2}+a_{3}+... +a_{n}$,则$S_{12}=$(A
)A.$\frac {201}{182}$
B.$\frac {203}{180}$
C.$\frac {199}{198}$
D.$\frac {203}{184}$
答案:
A
5. 有一列数:$-\frac {1}{2},\frac {1}{5},-\frac {1}{8},\frac {1}{11},... $,则第n个数是
$\frac{(-1)^n}{3n-1}$
。
答案:
$\frac{(-1)^n}{3n-1}$
6. 猜数字游戏中,小明写出如下一组数:$\frac {2}{5},\frac {4}{7},\frac {8}{11},\frac {16}{19},\frac {32}{35},... $,小亮猜测出第六个数是$\frac {64}{67}$,根据此规律,第n(n为正整数)个数是
$\frac{2^n}{2^n+3}$
。
答案:
$\frac{2^n}{2^n+3}$
7. 观察下列等式:①$9-4= 5$,②$25-16= 9$,③$49-36= 13$,④$81-64= 17$,…,则第n个等式为:
$(2n+1)^2-(2n)^2=4n+1$
(n为正整数)。
答案:
$(2n+1)^2-(2n)^2=4n+1$
8. 已知$a_{n}= \frac {1}{(n+1)^{2}}(n= 1,2,3,... )$,记$b_{1}= 2(1-a_{1}),b_{2}= 2(1-a_{1})(1-a_{2}),...,b_{n}= 2(1-a_{1})\cdot (1-a_{2})\cdot ... \cdot (1-a_{n})$,通过计算推测出$b_{n}= $
$\frac{n+2}{n+1}$
。(用含n的代数式表示)
答案:
$\frac{n+2}{n+1}$
9. 观察下列等式:$1^{3}= 1^{2},1^{3}+2^{3}= 3^{2},1^{3}+2^{3}+3^{3}= 6^{2},1^{3}+2^{3}+3^{3}+4^{3}= 10^{2},... $,根据等式左边各项幂的底数与等式右边幂的底数的关系,写出第n个等式:____
$1^3+2^3+3^3+\cdots+n^3=\left[\frac{n(n+1)}{2}\right]^2$
。
答案:
$1^3+2^3+3^3+\cdots+n^3=\left[\frac{n(n+1)}{2}\right]^2$
查看更多完整答案,请扫码查看


