《2025年启东中学作业本七年级数学上册苏科版徐州专版》

9. 给下列多项式添括号.使它们的最高次项系数变为正数：
(1)$-x^{2} + x =$$-(x^{2}-x)$；
(2)$3x^{2} - 2xy^{2} + 2y^{2} =$$-(2xy^{2}-3x^{2}-2y^{2})$；
(3)$-a^{3} + 2a^{2} - a + 1 =$$-(a^{3}-2a^{2}+a-1)$；
(4)$-3x^{2}y^{2} - 2x^{3} + y^{3} =$$-(3x^{2}y^{2}+2x^{3}-y^{3})$.

答案：
(1)$-(x^{2}-x)$；
(2)$-(2xy^{2}-3x^{2}-2y^{2})$；
(3)$-(a^{3}-2a^{2}+a-1)$；
(4)$-(3x^{2}y^{2}+2x^{3}-y^{3})$

10. 当$1 ＜ a ＜ 3$时，化简$|a - 3| + |1 - a|$的结果为____.

答案： 2

11. 先去括号，再合并同类项：
(1)$5(x + y) - 3(2x - 3y)$；
(2)$4a^{2} + 2(3ab - 2a^{2}) - (7ab - 1)$；
(3)$2(xy^{2} - 3x^{2}y) - 3(xy^{2} - 2x^{2}y)$；
(4)$3x - [5x - (\frac{1}{2}x - 4)]$.

答案： 解:
(1)原式=5x+5y-6x+9y=-x+14y；
(2)原式=$4a^{2}+6ab-4a^{2}-7ab+1=-ab+1$；
(3)原式=$2xy^{2}-6x^{2}y-3xy^{2}+6x^{2}y=-xy^{2}$；
(4)原式=$3x-(5x-\frac{1}{2}x+4)=3x-5x+\frac{1}{2}x-4=-\frac{3}{2}x-4$

12. 小波准备完成题目：化简$(□x^{2} + 6x + 8) - (6x + 5x^{2} + 2)$时，发现系数“$□$”印刷不清楚.
(1)他把“$□$”猜成3，请化简：$(3x^{2} + 6x + 8) - (6x + 5x^{2} + 2)$；
(2)他妈妈说：“你猜错了，我看到该题标准答案的结果是常数.”通过计算说明原题中“$□$”是多少.

答案：
(1)原式=$3x^{2}+6x+8-6x-5x^{2}-2=-2x^{2}+6$；
(2)设“□”为a,原式=$(a-5)x^{2}+6$,当a=5时,原式的结果为常数,所以“□”为5

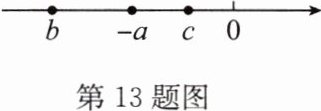
13. 已知$-a$，$b$，$c$在数轴上的位置如图.
(1)填空：$c$＜0，$c - b$＞0，$a + b$＜0；（填“$＞$”“$＜$”或“$=$”）
(2)化简：$|c| - |c - b|$；
解:原式=-c-c+b=b-2c
(3)化简：$|c| - |c - b| + |a - c| + |a + b|$.
解:原式=-c-c+b+a-c-a-b=-3c

答案：
(1)＜ ＞ ＜；
(2)解:原式=-c-c+b=b-2c；
(3)解:原式=-c-c+b+a-c-a-b=-3c