《2025年暑假衔接七年级数学浙教版延边人民出版社》

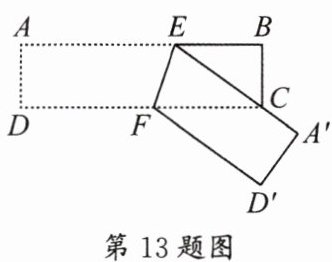
13. 如图,长方形纸带 $ ABCD $,$ AB // CD $,将纸带沿 $ EF $ 折叠,点 $ A $,$ D $ 分别与点 $ A' $,$ D' $ 对应,若 $ ∠CFE = 2∠CFD' $,则 $ ∠AEF $ 的度数是______72°。

答案： $72^{\circ }$【解析】因为$AB// CD$，所以$∠CFE=∠AEF$，又因为翻折，所以$∠DFE=∠D'FE$，因为$∠CFE=2∠CFD'$，所以$∠DFE=∠D'FE=3∠CFD'$，所以$∠DFE+∠CFE=3∠CFD'+2∠CFD'=180^{\circ }$，所以$∠CFD'=36^{\circ }$，所以$∠AEF=∠CFE=2∠CFD'=72^{\circ }$。故答案为：$72^{\circ }$。

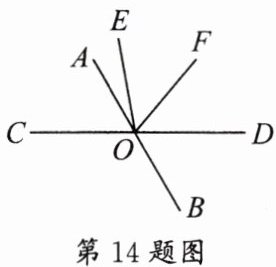
14. 如图,直线 $ AB $ 与 $ CD $ 相交于点 $ O $,$ ∠AOC - 2∠AOE = 20^{\circ} $,射线 $ OF $ 平分 $ ∠DOE $,若 $ ∠BOD = 60^{\circ} $,则 $ ∠AOF = $$70^{\circ }$。

答案： $70^{\circ }$【解析】因为$∠AOC$与$∠BOD$是对顶角，所以$∠AOC=∠BOD=60^{\circ }$，所以$∠AOD=180^{\circ }-∠AOC=120^{\circ }$，因为$∠AOC-2∠AOE=20^{\circ }$，所以$∠AOE=20^{\circ }$，所以$∠DOE=∠AOD-∠AOE=100^{\circ }$，因为射线$OF$平分$∠DOE$，所以$∠DOF=\frac {1}{2}∠DOE=50^{\circ }$，所以$∠AOF=∠AOD-∠DOF=120^{\circ }-50^{\circ }=70^{\circ }$，故答案为：$70^{\circ }$。

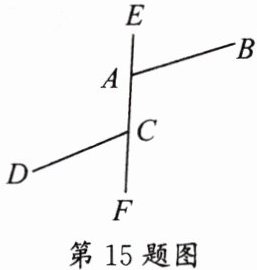
15. 如图,直线 $ EF $ 上有 $ A $,$ C $ 两点,分别引两条射线 $ AB $,$ CD $,$ ∠BAF = 110^{\circ} $,$ ∠DCF = 60^{\circ} $,射线 $ AB $,$ CD $ 分别绕点 $ A $,点 $ C $ 以 $ 1 $ 度/秒和 $ 3 $ 度/秒的速度同时顺时针转动,设时间为 $ t $,在射线 $ CD $ 转动一周的时间内,当 $ CD $ 与 $ AB $ 平行时,所有满足条件的时间 $ t = $______秒。

答案：
5 或 95 【解析】因为$∠DCF=60^{\circ }$，所以$∠ACD=180^{\circ }-∠DCF=180^{\circ }-60^{\circ }=120^{\circ }$，分三种情况：如图 1，$AB$与$CD$在$EF$的两侧时，$∠ACD=120^{\circ }-(3t)^{\circ },∠BAC=110^{\circ }-t^{\circ }$，要使$AB// CD$，则$∠ACD=∠BAC$，即$120^{\circ }-(3t)^{\circ }=110^{\circ }-t^{\circ }$，解得$t=5$；如图 2，$CD$旋转到与$AB$都在$EF$的右侧时，$∠DCF=360^{\circ }-(3t)^{\circ }-60^{\circ }=300^{\circ }-(3t)^{\circ },∠BAC=110^{\circ }-t^{\circ }$，要使$AB// CD$，则$∠DCF=∠BAC$，即$300^{\circ }-(3t)^{\circ }=110^{\circ }-t^{\circ }$，解得$t=95$；如图 3，$CD$旋转到与$AB$都在$EF$的左侧时，$∠DCF=(3t)^{\circ }-(180^{\circ }-60^{\circ }+180^{\circ })=(3t)^{\circ }-300^{\circ },∠BAC=t^{\circ }-110^{\circ }$，要使$AB// CD$，则$∠DCF=∠BAC$，即$(3t)^{\circ }-300^{\circ }=t^{\circ }-110^{\circ }$，解得$t=95$，此时$∠BAC=t^{\circ }-110^{\circ }＜0^{\circ }$，所以此情况不存在。综上所述，当时间$t$的值为 5 秒或 95 秒时，$CD$与$AB$平行。故答案为：5 或 95。

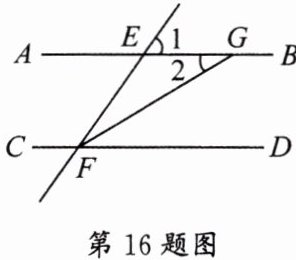
16. 如图,已知：$ AB // CD $,$ ∠1 = 58^{\circ} $,$ FG $ 平分 $ ∠EFD $,求 $ ∠2 $ 的度数。

解：因为$AB// CD$，所以$∠EFD=∠1=58^{\circ }$，因为$FG$平分$∠EFD$，所以$∠GFD=\frac {1}{2}∠EFD=\frac {1}{2}×58^{\circ }=29^{\circ }$，因为$AB// CD$，所以$∠2=∠GFD=29°$。

答案： 因为$AB// CD$，所以$∠EFD=∠1=58^{\circ }$，因为$FG$平分$∠EFD$，所以$∠GFD=\frac {1}{2}∠EFD=\frac {1}{2}×58^{\circ }=29^{\circ }$，因为$AB// CD$，所以$∠2=∠GFD=29^{\circ }$。

17. 如图,已知 $ ∠1 = ∠2 $,$ ∠4 = ∠B $,$ ∠ADF = 90^{\circ} $,试说明：$ GF ⊥ BC $。
阅读下面的解答过程,填空并填写理由。
解：因为 $ ∠4 = ∠B $(已知),
所以 $ AB // $$DE$(同位角相等，两直线平行)。
所以 $ ∠2 = ∠3 $(两直线平行，内错角相等)。
因为 $ ∠1 = ∠2 $(已知),
所以 $ ∠1 = ∠3 $(等量代换)。
所以 $ AD // $$GF$(同位角相等，两直线平行)。
所以 $ ∠ADF + ∠GFD = $$180^{\circ }$(两直线平行，同旁内角互补)。
又因为 $ ∠ADF = 90^{\circ} $(已知),
所以 $ ∠GFD = 90^{\circ} $。
所以 $ GF ⊥ BC $(垂直的定义)。

答案： $DE$ 同位角相等，两直线平行 两直线平行，内错角相等 等量代换 $GF$ 同位角相等，两直线平行 $180^{\circ }$ 两直线平行，同旁内角互补 垂直的定义