2025年暑假衔接七年级数学浙教版延边人民出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假衔接七年级数学浙教版延边人民出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第26页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
1. 如图,在边长为$a的正方形中挖掉一个边长为b$的小正方形,把余下的部分剪成两个直角梯形后,再拼成一个长方形,通过计算阴影部分的面积,验证了一个等式,这个等式是……………………………………………………………………(
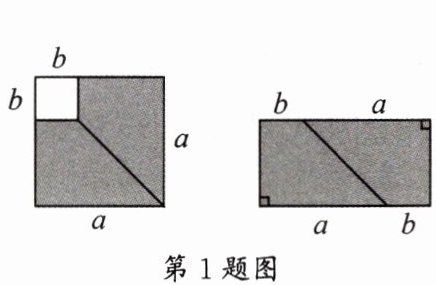
A. $a^{2}-b^{2}= (a+b)(a-b)$
B. $(a+b)^{2}= a^{2}+2ab+b^{2}$
C. $(a-b)^{2}= a^{2}-2ab+b^{2}$
D. $a^{2}-ab= a(a-b)$
A
)
A. $a^{2}-b^{2}= (a+b)(a-b)$
B. $(a+b)^{2}= a^{2}+2ab+b^{2}$
C. $(a-b)^{2}= a^{2}-2ab+b^{2}$
D. $a^{2}-ab= a(a-b)$
答案:
A
2. 将几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式。例如,由图1可得等式:$x^{2}+(p+q)x+pq= (x+p)(x+q)$,将图2所示的卡片若干进行拼图,可以将二次三项式$a^{2}+4ab+3b^{2}$分解因式为……………………………………………………………………(
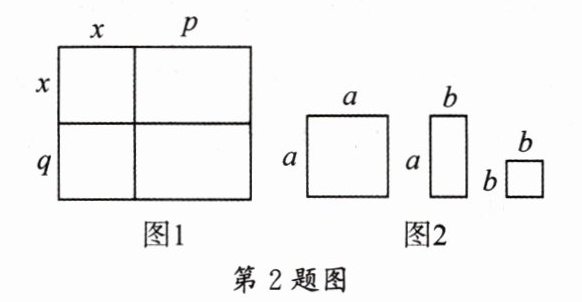
A. $(a+b)(2a+b)$
B. $(a+b)(3a+b)$
C. $(a+b)(a+2b)$
D. $(a+b)(a+3b)$
D
)
A. $(a+b)(2a+b)$
B. $(a+b)(3a+b)$
C. $(a+b)(a+2b)$
D. $(a+b)(a+3b)$
答案:
D
3. 在学习“因式分解”时,邹老师给同学们发了很多硬纸片($a×a的正方形A$,$b×b的正方形B$,$a×b的长方形C$)。
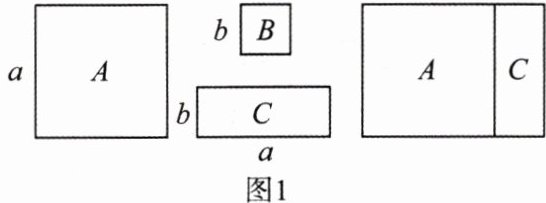
(1)在探究中,小明用1张$A$和1张$C$组成如图1所示的长方形可以说明$a^{2}+ab$可以分解为____。
(2)继续探究中,小明用1张$A$,2张$B$和3张$C$再次拼得一个长方形,请在图2中画出示意图,并将长方形面积表达式的因式分解结果写在横线上。
(3)尝试应用:请你仿照小明同学的探究方法,尝试用1张$A$,4张$B和若干张C$拼成一个长方形或者正方形,请你设计两种不同的拼法,在图3和图4中分别画出示意图,并在相应的横线上写出所拼长方形的面积表达式及因式分解的结果。


(1)在探究中,小明用1张$A$和1张$C$组成如图1所示的长方形可以说明$a^{2}+ab$可以分解为____。
(2)继续探究中,小明用1张$A$,2张$B$和3张$C$再次拼得一个长方形,请在图2中画出示意图,并将长方形面积表达式的因式分解结果写在横线上。
(3)尝试应用:请你仿照小明同学的探究方法,尝试用1张$A$,4张$B和若干张C$拼成一个长方形或者正方形,请你设计两种不同的拼法,在图3和图4中分别画出示意图,并在相应的横线上写出所拼长方形的面积表达式及因式分解的结果。

答案:
(1)$a(a + b)$
(2)$a^{2}+3ab + 2b^{2}=(a + b)(a + 2b)$,故答案为:$(a + b)(a + 2b)$,示意图如图1。
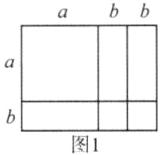
(3)示意图如图2 $a^{2}+4b^{2}+4ab=(a + 2b)^{2}$ 示意图如图3 $a^{2}+4b^{2}+5ab=(a + b)(a + 4b)$

(1)$a(a + b)$
(2)$a^{2}+3ab + 2b^{2}=(a + b)(a + 2b)$,故答案为:$(a + b)(a + 2b)$,示意图如图1。

(3)示意图如图2 $a^{2}+4b^{2}+4ab=(a + 2b)^{2}$ 示意图如图3 $a^{2}+4b^{2}+5ab=(a + b)(a + 4b)$

查看更多完整答案,请扫码查看


