《2025年一本九年级物理全一册人教版重庆专版》

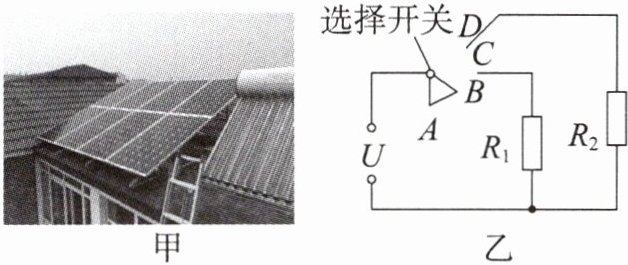
典例1 (2024·外国语学校三模)如图甲所示，为响应国家“绿色新能源、低碳环保”的号召，某地区利用当地丰富的太阳能资源进行光伏发电，供生产、生活使用。小明家将太阳能转化的电能储存到电源中，给电热水壶和电暖器供电，简化电路如图乙所示。$R_{1}$和$R_{2}$是阻值恒定的发热电阻，电热水壶的加热电阻$R_{1}$标有“220 V 484 W”字样，电暖器的加热电阻$R_{2}$标有“220 V 2 420 W”字样。已知太阳能照射到电池板的辐射功率为$500J/(s\cdot m^{2})$（即1s内辐射在$1m^{2}$太阳能电池板上的太阳能为500 J），太阳能电池板将太阳能直接转化为电能的效率为20%。
(1)求加热电阻$R_{1}$的阻值为100Ω。
(2)若小明家太阳能电池板的有效面积为$4m^{2}$，10 min内通过该太阳能电池板获得的电能为2.4×10^{5}J。
(3)若电热水壶和电暖器同时工作时，$R_{1}$每分钟放出$2.4×10^{4}J$的热量，$R_{2}$的实际加热功率为2000W。

答案： #### 典例 1 解：
(1) 加热电阻 $ R_{1} $ 的阻值
$ R_{1} = \frac{U^{2}}{P_{1}} = \frac{(220\ \text{V})^{2}}{484\ \text{W}} = 100\ \Omega $
(2) 有效面积为 $ 4\ \text{m}^{2} $ 的太阳能电池板 $ 10\ \text{min} $ 接收的太阳能 $ E_{\text{太阳能}} = 500\ \text{J}/(\text{s} \cdot \text{m}^{2}) \times 4\ \text{m}^{2} \times 10 \times 60\ \text{s} = 1.2 \times 10^{6}\ \text{J} $
因太阳能电池板将太阳能直接转化为电能的效率为 $ 20\% $，所以 $ 10\ \text{min} $ 内通过该太阳能电池板获得的电能
$ W = 20\% E_{\text{太阳能}} = 20\% \times 1.2 \times 10^{6}\ \text{J} = 2.4 \times 10^{5}\ \text{J} $
(3) 若电热水壶和电暖器同时工作，两发热电阻是并联的。
发热电阻 $ R_{2} $ 的阻值 $ R_{2} = \frac{U^{2}}{P_{2}} = \frac{(220\ \text{V})^{2}}{2420\ \text{W}} = 20\ \Omega $
$ R_{1} $ 每分钟放出 $ 2.4 \times 10^{4}\ \text{J} $ 的热量，则此时 $ R_{1} $ 的实际加热功率
$ P_{\text{实}1} = \frac{W_{1}}{t} = \frac{Q_{1}}{t} = \frac{2.4 \times 10^{4}\ \text{J}}{60\ \text{s}} = 400\ \text{W} $
由并联电路电压特点和 $ P = \frac{U^{2}}{R} $ 可知
$ \frac{P_{\text{实}1}}{P_{\text{实}2}} = \frac{\frac{U_{\text{实}}^{2}}{R_{1}}}{\frac{U_{\text{实}}^{2}}{R_{2}}} = \frac{R_{2}}{R_{1}} = \frac{20\ \Omega}{100\ \Omega} = \frac{1}{5} $
所以 $ P_{\text{实}2} = 5P_{\text{实}1} = 5 \times 400\ \text{W} = 2000\ \text{W} $

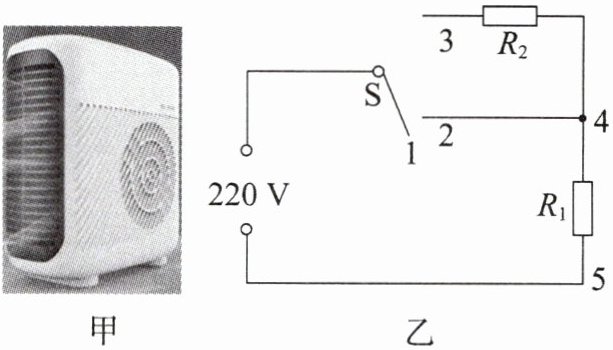
典例2 (2024·西大附中三模)图甲是小彭家中的迷你双控温暖风机，其内部加热部分简化电路如图乙所示，$R_{1}$和$R_{2}$是加热电阻，该暖风机正常工作时低温挡的加热功率为242 W，高温挡的加热功率是低温挡的4倍。求：
(1)低温挡的电流为1.1 A；
(2)加热电阻$R_{2}$的阻值为150 Ω；
(3)不改变原电路已有的元件位置，想在原电路中某处再新增一个加热电阻，使高温挡的功率变为原来的1.5倍，请说明该电阻连接的位置和方式(串联或并联)，并计算新增的加热电阻的阻值大小。
答：应在4和5之间并联一个加热电阻，新增的加热电阻的阻值大小为100 Ω。

答案： #### 典例 2 解：
(1) 低温挡的电流 $ I = \frac{P_{\text{低温}}}{U} = \frac{242\ \text{W}}{220\ \text{V}} = 1.1\ \text{A} $
(2) 高温挡的加热功率是低温挡的 $ 4 $ 倍，则 $ P_{\text{高温}} = 968\ \text{W} $
开关 $ S $ 接 $ 2 $ 时，电路为只含有 $ R_{1} $ 的简单电路，总电阻较小，总功率较大，该暖风机处于高温挡，则电阻 $ R_{1} $ 的阻值
$ R_{1} = \frac{U^{2}}{P_{\text{高温}}} = \frac{(220\ \text{V})^{2}}{968\ \text{W}} = 50\ \Omega $
开关 $ S $ 接 $ 3 $ 时，两电阻串联，总电阻较大，总功率较小，该暖风机处于低温挡，则两电阻之和
$ R_{\text{串}} = \frac{U^{2}}{P_{\text{低温}}} = \frac{(220\ \text{V})^{2}}{242\ \text{W}} = 200\ \Omega $
加热电阻 $ R_{2} $ 的阻值 $ R_{2} = R_{\text{串}} - R_{1} = 200\ \Omega - 50\ \Omega = 150\ \Omega $
(3) 开关 $ S $ 接 $ 2 $ 时，电路中只有 $ R_{1} $ 工作，该暖风机处于高温挡。要使高温挡的功率变为原来的 $ 1.5 $ 倍，由 $ P = \frac{U^{2}}{R} $ 可知，应减小高温挡的电阻，可在 $ 4 $ 和 $ 5 $ 之间并联一个加热电阻，增加的功率 $ \Delta P = 0.5P_{\text{高温}} = 0.5 \times 968\ \text{W} = 484\ \text{W} $
新增电阻的阻值 $ R_{x} = \frac{U^{2}}{\Delta P} = \frac{(220\ \text{V})^{2}}{484\ \text{W}} = 100\ \Omega $