《2025年畅行课堂九年级数学下册人教版山西专版》

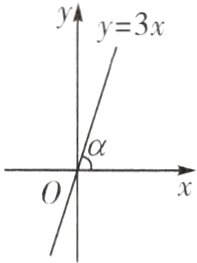
6. 在平面直角坐标系中，直线y = 3x与x轴的夹角为α，求α的正弦值和余弦值.

答案：
解：如图，在直线y = 3x上任取一点P（与点O不重合），过点P作PA⊥x轴于点A. 设点P的横坐标为a（a≠0），则该点的纵坐标为3a，

所以在Rt△POA中，OA = |a|，AP = |3a|.
由勾股定理，得OP = $\sqrt{(3a)^{2}+a^{2}}$ = $\sqrt{10}|a|$，
所以sinα = $\frac{PA}{OP}$ = $\frac{3|a|}{\sqrt{10}|a|}$ = $\frac{3\sqrt{10}}{10}$，
cosα = $\frac{|a|}{\sqrt{10}|a|}$ = $\frac{\sqrt{10}}{10}$.

7.（2024·济南）城市轨道交通发展迅猛，为市民出行带来极大方便. 某校“综合实践”小组想测得轻轨高架站的相关距离，数据勘测组通过勘测得到了如下记录表：

请根据记录表提供的信息完成下列问题：
（1）求点C到地面DE的距离；
（2）求顶部线段BC的长.
（结果精确到0.01 m，参考数据：sin15°≈0.259，cos15°≈0.966，tan15°≈0.268，sin83°≈0.993，cos83°≈0.122，tan83°≈8.144）

答案：
解：
(1) 如图，过点C作CN⊥ED，交ED的延长线于点N.
∵∠CDE = 97°，
∴∠CDN = 83°.
在Rt△CDN中，
∵sin∠CDN = sin83° = $\frac{CN}{CD}$≈0.993，CD = 6.7 m，
∴CN = CD·sin83°≈6.7×0.993≈6.65(m).
答：点C到地面DE的距离约为6.65 m.

(2) 如图，过点B作BP⊥CF，垂足为P.
∵CF//DE，
∴∠FCD = ∠CDN = 83°.
∵∠BCD = 98°，
∴∠BCP = ∠BCD - ∠FCD = 15°.
∵平行线间的距离处处相等，
∴EF = CN = 6.65 m.
∵AE = 8.5 m，
∴BP = AF = AE - EF = 8.5 - 6.65 = 1.85.
在Rt△BPC中，
∵sin∠BCP = $\frac{BP}{BC}$ = sin15°≈0.259，
∴BC = $\frac{BP}{sin15^{\circ}}$≈$\frac{1.85}{0.259}$≈7.14(m).
答：顶部线段BC的长约为7.14 m.

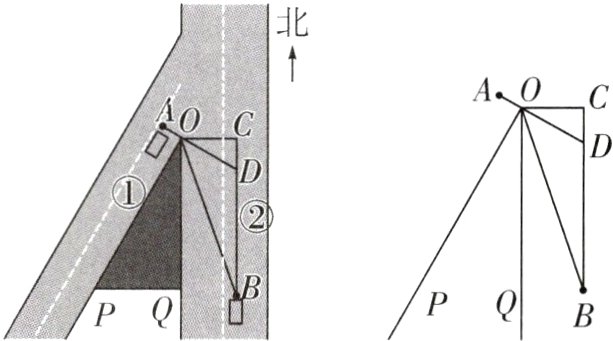
8.（2023·株洲）如图所示，在某交叉路口，一辆货车在道路①上点A处等候“绿灯”，一辆车从被山峰POQ遮挡的道路②的点B处由南向北行驶. 已知∠POQ = 30°，BC//OQ，OC⊥OQ，AO⊥OP，线段AO的延长线交直线BC于点D.
（1）求∠COD的大小；
（2）若在点B处测得点O在北偏西α方向上，其中tanα = $\frac{\sqrt{3}}{5}$，OD = 12米. 问该轿车至少行驶多少米才能发现点A处的货车？（当该轿车行驶至点D处时，正好发现点A处的货车）

答案： 解：
(1)
∵AO⊥OP，
∴∠POD = 90°.
∵∠POQ = 30°，
∴∠DOQ = ∠POD - ∠POQ = 90° - 30° = 60°.
∵OC⊥OQ，
∴∠COQ = 90°，
∴∠COD = ∠COQ - ∠DOQ = 90° - 60° = 30°，
即∠COD的大小为30°.
(2)
∵BC//OQ，
∴∠BCO = 180° - ∠COQ = 90°.
在Rt△COD中，∠COD = 30°，OD = 12米，
∴CD = $\frac{1}{2}$OD = 6米，
∴OC = $\sqrt{OD^{2}-CD^{2}}$ = $\sqrt{12^{2}-6^{2}}$ = 6$\sqrt{3}$(米).
∵tanα = tan∠OBC = $\frac{\sqrt{3}}{5}$ = $\frac{OC}{BC}$，
∴BC = 6$\sqrt{3}$÷$\frac{\sqrt{3}}{5}$ = 30(米).
∴BD = BC - CD = 30 - 6 = 24(米).
答：该轿车至少行驶24米才能发现点A处的货车.