《2025年畅行课堂九年级数学下册人教版山西专版》

10.(2023·山西模拟)某校课外活动小组来到太原古县城进行参观研学，对位于古县城“十字街”的旗亭高度进行了实地测量。项目操作过程如下：
如图，测试小组利用测角仪从点D处观测旗亭顶端A点的仰角为24°。在测角仪和旗亭之间水平光滑的地面放置一个平面镜，小组成员在平面镜上做好标记后，将平面镜在地面上来回移动，当平面镜上的标记位于点E处时，观测的同学恰好能从点D处看到旗亭顶端A在镜子中的像与平面镜上的标记重合，此时测得CE = 2米。已知测角仪的高度CD = 1米，点A，B，C，D，E在同一竖直平面内，且点B，E，C在同一条水平直线上，求旗亭AB的高度。（结果精确到1米，参考数据：$\tan24^{\circ}\approx0.45$，$\sin24^{\circ}\approx0.41$，$\cos24^{\circ}\approx0.91$）
　

答案：
解：如图，过点D作DF⊥AB于点F，则四边形BFDC为矩形，
∴BF = DC，DF = BC，

根据题意，得∠AEB = ∠DEC.
在Rt△CDE中，tan∠DEC = $\frac{CD}{CE}$ = $\frac{1}{2}$，
∴tan∠AEB = $\frac{AB}{BE}$ = $\frac{1}{2}$.
设AB = x米，则BE = 2x米，AF = (x - 1)米，DF = (2x + 2)米.
在Rt△ADF中，tan∠ADF = tan24° = $\frac{AF}{DF}$，
即$\frac{x - 1}{2x + 2}$ ≈ 0.45，解得x ≈ 19.
答：旗亭AB的高度约为19米.

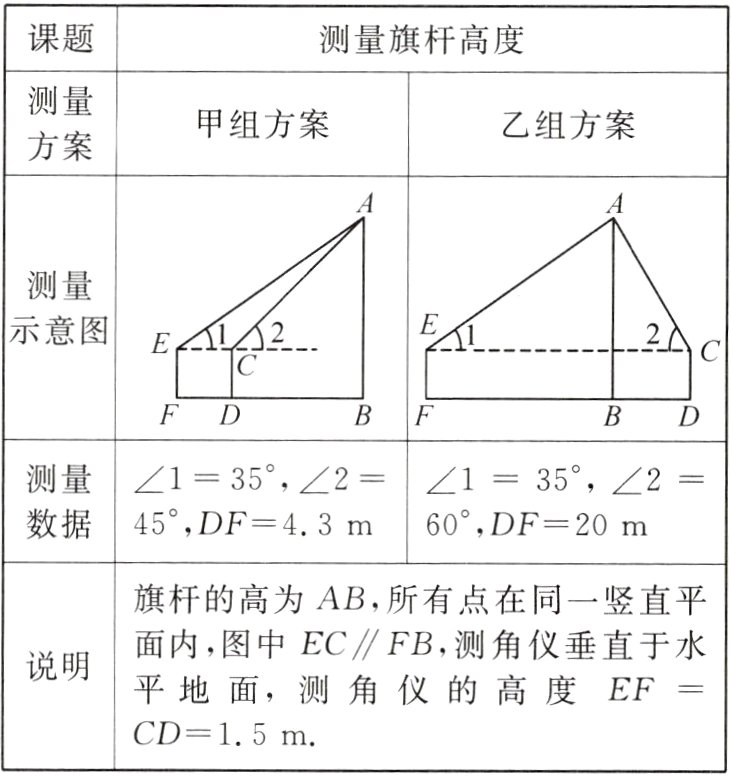
11.【项目式学习】(2022·贵阳清镇市模拟)某数学兴趣小组把测量学校内旗杆的高度作为一次课题活动，甲、乙两组同学分别制定了不同的测量方案，并完成了实地测量，测量方案与数据如下表：
请任选一种方案计算旗杆的高度。（结果精确到0.1 m）（参考数据：$\sin35^{\circ}\approx0.57$，$\cos35^{\circ}\approx0.82$，$\tan35^{\circ}\approx0.70$，$\sqrt{2}\approx1.41$，$\sqrt{3}\approx1.73$）
　

答案：
解：选甲组方案，如图，过点C作CH⊥AB于点H.

根据题意，可知点E，C，H在同一条直线上.
∵EC//FB，CD//EF，CD//BH，
∴四边形EFDC和四边形BDCH均为平行四边形，
∴BH = CD = 1.5 m，CE = DF = 4.3 m.
∵∠2 = 45°，
∴CH = AH.
设AH = CH = x m，
则EH = CE + CH = (4.3 + x)m，
在Rt△AEH中，
tan∠1 = tan35° = $\frac{AH}{EH}$ = $\frac{x}{4.3 + x}$ ≈ 0.70，
解得x ≈ 10.0，即AH = 10.0 m，
∴AB = AH + BH ≈ 10.0 + 1.5 = 11.5(m).
答：旗杆的高度约为11.5 m.