《2025年畅行课堂九年级数学下册人教版山西专版》

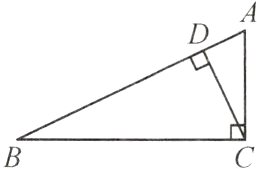
11.【教材九下P69习题T6变式】如图，在Rt△ABC中，CD是斜边AB上的高，∠B≠45°，则下列比值中不等于cosB的是（ ）

A.$\frac{BD}{BC}$
B.$\frac{BC}{AB}$
C.$\frac{AD}{AC}$
D.$\frac{CD}{AC}$

答案： C

12.(安顺中考)如图，半径为3的⊙A经过原点O和点C(0，2)，B是y轴左侧⊙A优弧上一点，则tan∠OBC为（ ）
　　　
A.$\frac{1}{3}$
B.2$\sqrt{2}$
C.$\frac{2\sqrt{2}}{3}$
D.$\frac{\sqrt{2}}{4}$

答案： D

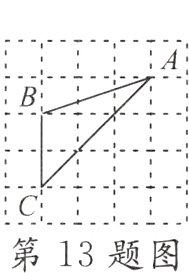
13.(乐山中考)如图，已知△ABC的三个顶点均在格点上，则cosA的值为________.

答案： $\frac{2\sqrt{5}}{5}$

14.如图，将矩形ABCD沿EF折叠，使顶点C恰好落在边AB的中点C′处.若AB = 4，BC = 8，则tan∠BFC′的值为________.

答案： $\frac{8}{15}$

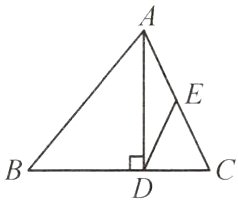
15.【转化思想】如图，在△ABC中，AD是边BC上的高，E为AC的中点，BC = 14，AD = 12，sinB = $\frac{4}{5}$.求：
(1)线段CD的长；
(2)tan∠EDC的值.

答案： 解：
(1)$\because AD$是边$BC$上的高，
$\therefore\triangle ADB$为直角三角形.
$\because AD = 12$，$\sin B=\frac{AD}{AB}=\frac{4}{5}$，
$\therefore AB=\frac{AD}{\sin B}=\frac{12}{\frac{4}{5}} = 15$，
$\therefore BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{15^{2}-12^{2}} = 9$，
$\therefore CD = BC - BD = 14 - 9 = 5$.
(2)$\because E$是Rt△ADC斜边$AC$的中点，
$\therefore DE=\frac{1}{2}AC = EC$.$\therefore\angle EDC=\angle C$.
$\therefore\tan\angle EDC=\tan C=\frac{AD}{CD}=\frac{12}{5}$.

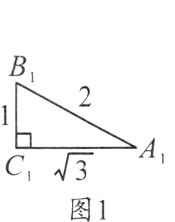
16.如图，根据图中数据完成填空，再按要求解答下列问题：

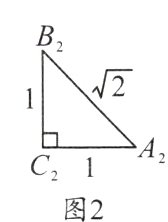
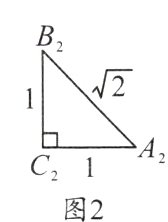
sin²A₁ + sin²B₁ = ______；sin²A₂ + sin²B₂ = ______；sin²A₃ + sin²B₃ = ______.
(1)观察上述等式，猜想：在Rt△ABC中，当∠C = 90°时，sin²A + sin²B = ______；
(2)如图4，在Rt△ABC中，∠C = 90°，∠A，∠B，∠C的对边分别是a，b，c，利用三角函数的定义和勾股定理，证明你的猜想；
(3)已知∠A + ∠B = 90°，且sinA = $\frac{5}{13}$，求sinB的值.

答案： 1 1 1
(1)1
(2)证明：根据题意，得$\sin A=\frac{a}{c}$，
$\sin B=\frac{b}{c}$，
$\therefore\sin^{2}A+\sin^{2}B=\frac{a^{2}+b^{2}}{c^{2}}$.
由勾股定理，得$a^{2}+b^{2}=c^{2}$，
$\therefore\sin^{2}A+\sin^{2}B = 1$.
(3)解：$\because\angle A+\angle B = 90^{\circ}$.
$\therefore\sin^{2}A+\sin^{2}B = 1$.
又$\because\sin A=\frac{5}{13}$，
$\therefore\sin B=\sqrt{1 - (\frac{5}{13})^{2}}=\frac{12}{13}$.