2025年畅行课堂九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年畅行课堂九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
12.(2023·吕梁一模)近年来,随着智能技术的发展,智能机器人已经服务于社会生活的各个方面.如图1所示的是一款智能送货机器人,图2是其侧面示意图,现测得其矩形底座ABCD的高BC为30 cm,上部显示屏EF的长度为30 cm,侧面支架EC的长度为100 cm,∠ECD = 80°,∠FEC = 130°,则该机器人的最高点F距地面AB的高度约为 __________.(结果精确到1 cm,参考数据:sin 80°≈0.98,cos 80°≈0.17,tan 80°≈5.67)

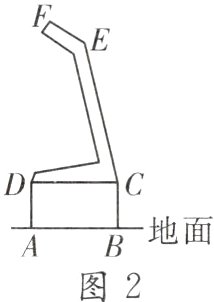


答案:
143 cm
13.(2023·张家界)“游张家界山水,逛七十二奇楼”成为今年旅游新特色.某数学兴趣小组用无人机测量奇楼AB的高度,测量方案如图:先将无人机垂直上升至距水平地面225 m的P点,测得奇楼顶端A的俯角为15°,再将无人机沿水平方向飞行200 m到达点Q,测得奇楼底端B的俯角为45°,求奇楼AB的高度.(结果精确到1 m,参考数据:sin 15°≈0.26,cos 15°≈0.97,tan 15°≈0.27)
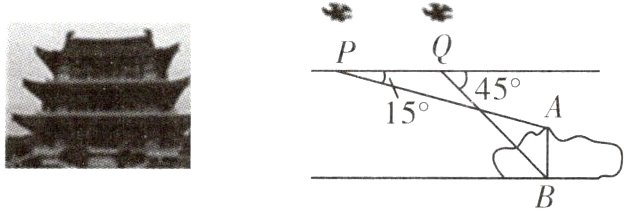

答案:
解:如图,延长 BA 交 PQ 的延长线于点 C,则∠BCQ = 90°.

根据题意,得 BC = 225 m,PQ = 200 m.
在 Rt△BCQ 中,∠BQC = 45°,
∴CQ = BC = 225 m,
∴PC = PQ + CQ = 425 m.
在 Rt△PCA 中,
tan∠APC = tan 15° = $\frac{AC}{PC}$ = $\frac{AC}{425}$ ≈ 0.27,
∴AC ≈ 114.75 m,
∴AB = BC - AC ≈ 225 - 114.75 = 110.25 ≈ 110(m).
答:奇楼 AB 的高度约为 110 m.
解:如图,延长 BA 交 PQ 的延长线于点 C,则∠BCQ = 90°.

根据题意,得 BC = 225 m,PQ = 200 m.
在 Rt△BCQ 中,∠BQC = 45°,
∴CQ = BC = 225 m,
∴PC = PQ + CQ = 425 m.
在 Rt△PCA 中,
tan∠APC = tan 15° = $\frac{AC}{PC}$ = $\frac{AC}{425}$ ≈ 0.27,
∴AC ≈ 114.75 m,
∴AB = BC - AC ≈ 225 - 114.75 = 110.25 ≈ 110(m).
答:奇楼 AB 的高度约为 110 m.
14.(2024·江西)图1是世界第一“大碗”——景德镇昌南里文化艺术中心主体建筑,其造型灵感来自于宋代湖田窑影青斗笠碗,寓意“万瓷之母”.如图2,“大碗”的主视图由“大碗”主体ABCD和矩形碗底BEFC组成,已知AD//EF,AM,DN是太阳光线,AM⊥MN,DN⊥MN,点M,E,F,N在同一条直线上.经测量ME = FN = 20.0 m,EF = 40.0 m,BE = 2.4 m,∠ABE = 152°.(结果精确到0.1 m)
(1)求“大碗”的口径AD的长;
(2)求“大碗”的高度AM的长.
(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
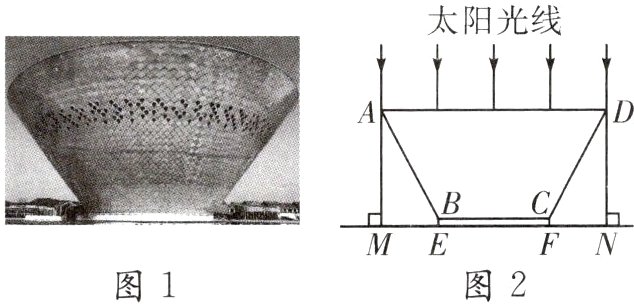
(1)求“大碗”的口径AD的长;
(2)求“大碗”的高度AM的长.
(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)

答案:
解:
(1)
∵AM⊥MN,DN⊥MN
∴∠AMN = ∠DNM = 90°.
∵AD//MN,
∴∠DAM = 180° - ∠AMN = 90°,
∴四边形 AMND 是矩形,
∴AD = MN = ME + EF + FN = 20.0 + 40.0 + 20.0 = 80.0(m).
答:“大碗”的口径 AD 的长为 80.0 m.
(2) 如图,延长 CB 交 AM 于点 G.

由题意,得 BE = GM = 2.4 m,BG = ME = 20.0 m,BG⊥AM,∠EBG = 90°,
∵∠ABE = 152°,
∴∠ABG = ∠ABE - ∠EBG = 62°.
在 Rt△AGB 中,AG = BG·tan62° ≈ 20.0×1.88 = 37.6(m),
∴AM = AG + MG = 37.6 + 2.4 = 40.0(m).
答:“大碗”的高度 AM 的长约为 40.0 m.
解:
(1)
∵AM⊥MN,DN⊥MN
∴∠AMN = ∠DNM = 90°.
∵AD//MN,
∴∠DAM = 180° - ∠AMN = 90°,
∴四边形 AMND 是矩形,
∴AD = MN = ME + EF + FN = 20.0 + 40.0 + 20.0 = 80.0(m).
答:“大碗”的口径 AD 的长为 80.0 m.
(2) 如图,延长 CB 交 AM 于点 G.

由题意,得 BE = GM = 2.4 m,BG = ME = 20.0 m,BG⊥AM,∠EBG = 90°,
∵∠ABE = 152°,
∴∠ABG = ∠ABE - ∠EBG = 62°.
在 Rt△AGB 中,AG = BG·tan62° ≈ 20.0×1.88 = 37.6(m),
∴AM = AG + MG = 37.6 + 2.4 = 40.0(m).
答:“大碗”的高度 AM 的长约为 40.0 m.
查看更多完整答案,请扫码查看


