2025年畅行课堂九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年畅行课堂九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
11. 如图,将△ABC沿着DE剪成一个小三角形ADE和一个四边形D'E'CB. 若DE//BC,四边形D'E'CB各边的长度如图所示,则剪出的小三角形ADE应是( )
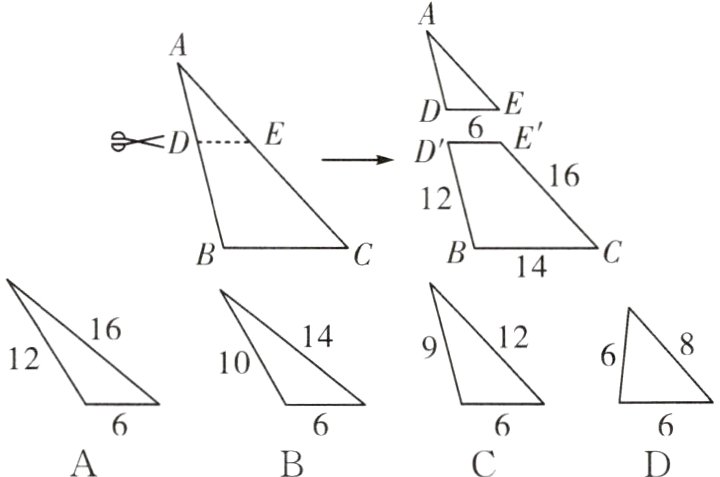

答案:
C
12.(2024·周口市扶沟县一模)五线谱是一种记谱法,通过在五根等距离的平行横线上标以不同时值的音符及其他记号来记载音乐. 如图,A,B,C为直线l与五线谱的横线相交的三个点,则$\frac{AB}{BC}$的值是____________.


答案:
2
13. 如图,点D是△ABC的边BC上一点,连接AD,过AD上的点E作EF//BD,交AB于点F,过点F作FG//AC,交BC于点G,已知$\frac{AE}{ED}=\frac{3}{2}$,BG = 4.
(1)求CG的长;
(2)若CD = 2,在上述条件和结论下,求EF的长.

(1)求CG的长;
(2)若CD = 2,在上述条件和结论下,求EF的长.

答案:
解:
(1)
∵EF//BD,
∴$\frac{AF}{FB}$=$\frac{AE}{ED}$=$\frac{3}{2}$.
∵FG//AC,
∴$\frac{BG}{CG}$=$\frac{BF}{AF}$=$\frac{2}{3}$.
∵BG=4,
∴CG=6.
(2)
∵CD=2,CG=6,
∴DG=CG−CD=4.
∵BG=4,
∴BD=BG+DG=8.
∵$\frac{AF}{BF}$=$\frac{3}{2}$,
∴$\frac{AF}{AB}$=$\frac{3}{5}$.
∵EF//BD,
∴$\frac{EF}{BD}$=$\frac{AF}{AB}$,即$\frac{EF}{8}$=$\frac{3}{5}$.
∴EF=$\frac{24}{5}$
(1)
∵EF//BD,
∴$\frac{AF}{FB}$=$\frac{AE}{ED}$=$\frac{3}{2}$.
∵FG//AC,
∴$\frac{BG}{CG}$=$\frac{BF}{AF}$=$\frac{2}{3}$.
∵BG=4,
∴CG=6.
(2)
∵CD=2,CG=6,
∴DG=CG−CD=4.
∵BG=4,
∴BD=BG+DG=8.
∵$\frac{AF}{BF}$=$\frac{3}{2}$,
∴$\frac{AF}{AB}$=$\frac{3}{5}$.
∵EF//BD,
∴$\frac{EF}{BD}$=$\frac{AF}{AB}$,即$\frac{EF}{8}$=$\frac{3}{5}$.
∴EF=$\frac{24}{5}$
【例】如图,AD是△ABC的中线.
(1)若点E为AD的中点,射线CE交AB于点F,则$\frac{AF}{BF}=$____________;
(2)若E为AD上的一点,且$\frac{AE}{ED}=\frac{1}{k}$,射线CE交AB于点F,则$\frac{AF}{BF}=$____________.
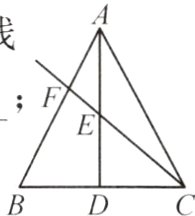
(1)若点E为AD的中点,射线CE交AB于点F,则$\frac{AF}{BF}=$____________;
(2)若E为AD上的一点,且$\frac{AE}{ED}=\frac{1}{k}$,射线CE交AB于点F,则$\frac{AF}{BF}=$____________.

答案:
(1)$\frac{1}{2}$
(2)$\frac{1}{2k}$
(1)$\frac{1}{2}$
(2)$\frac{1}{2k}$
【变式1】(梧州中考)如图,AG∶GD = 4∶1,BD∶DC = 2∶3,则AE与EC的比值是( )

A. 3∶2
B. 4∶3
C. 6∶5
D. 8∶5

A. 3∶2
B. 4∶3
C. 6∶5
D. 8∶5
答案:
D
【变式2】如图,BE是△ABC的中线,点F在BE上,延长AF交BC于点D. 若BF = 3EF,则$\frac{BD}{DC}=$____________.


答案:
$\frac{3}{2}$
14. 问题背景:
一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论. 如图1,已知AD是△ABC的角平分线,可证$\frac{AB}{AC}=\frac{BD}{CD}$. 小慧的证明思路是:如图2,过点C作CE//DA,交BA的延长线于点E,构造相似三角形来证明$\frac{AB}{AC}=\frac{BD}{CD}$.

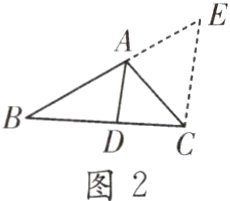
尝试证明:
(1)请参照小慧提供的思路,利用图2证明$\frac{AB}{AC}=\frac{BD}{CD}$;
应用拓展:
(2)如图3,在Rt△ABC中,∠BAC = 90°,D是边BC上一点. 连接AD,将△ACD沿AD所在直线折叠,点C恰好落在边AB上的点E处. 若AC = 1,AB = 2,求DE的长.

一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论. 如图1,已知AD是△ABC的角平分线,可证$\frac{AB}{AC}=\frac{BD}{CD}$. 小慧的证明思路是:如图2,过点C作CE//DA,交BA的延长线于点E,构造相似三角形来证明$\frac{AB}{AC}=\frac{BD}{CD}$.


尝试证明:
(1)请参照小慧提供的思路,利用图2证明$\frac{AB}{AC}=\frac{BD}{CD}$;
应用拓展:
(2)如图3,在Rt△ABC中,∠BAC = 90°,D是边BC上一点. 连接AD,将△ACD沿AD所在直线折叠,点C恰好落在边AB上的点E处. 若AC = 1,AB = 2,求DE的长.

答案:
(1)证明:
∵CE//DA,
∴$\frac{AB}{AE}$=$\frac{DB}{DC}$,∠DAC=∠ACE,∠BAD=∠E.
∵AD是△ABC的角平分线,
∴∠BAD=∠DAC,
∴∠ACE=∠E,
∴AC=AE,
∴$\frac{AB}{AC}$=$\frac{BD}{CD}$.
(2)解:由折叠的性质,得∠CAD=∠BAD,CD=DE.
由
(1),可知$\frac{AB}{AC}$=$\frac{BD}{CD}$,
∴$\frac{2}{1}$=$\frac{BD}{CD}$
∴BD=2CD.
∵∠BAC=90°,
∴BC=$\sqrt{AC^{2}+AB^{2}}$=$\sqrt{1^{2}+2^{2}}$=$\sqrt{5}$,
∴BD+CD=$\sqrt{5}$,
∴3CD=$\sqrt{5}$
∴CD=$\frac{\sqrt{5}}{3}$,
∴DE=$\frac{\sqrt{5}}{3}$
(1)证明:
∵CE//DA,
∴$\frac{AB}{AE}$=$\frac{DB}{DC}$,∠DAC=∠ACE,∠BAD=∠E.
∵AD是△ABC的角平分线,
∴∠BAD=∠DAC,
∴∠ACE=∠E,
∴AC=AE,
∴$\frac{AB}{AC}$=$\frac{BD}{CD}$.
(2)解:由折叠的性质,得∠CAD=∠BAD,CD=DE.
由
(1),可知$\frac{AB}{AC}$=$\frac{BD}{CD}$,
∴$\frac{2}{1}$=$\frac{BD}{CD}$
∴BD=2CD.
∵∠BAC=90°,
∴BC=$\sqrt{AC^{2}+AB^{2}}$=$\sqrt{1^{2}+2^{2}}$=$\sqrt{5}$,
∴BD+CD=$\sqrt{5}$,
∴3CD=$\sqrt{5}$
∴CD=$\frac{\sqrt{5}}{3}$,
∴DE=$\frac{\sqrt{5}}{3}$
查看更多完整答案,请扫码查看


