2025年畅行课堂九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年畅行课堂九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1.【几何直观】(攀枝花中考)如图,正比例函数$y = k_1x$与反比例函数$y = \frac{k_2}{x}$的图象交于$A(1,m),B$两点,当$k_1x\leqslant\frac{k_2}{x}$时,$x$的取值范围是( )
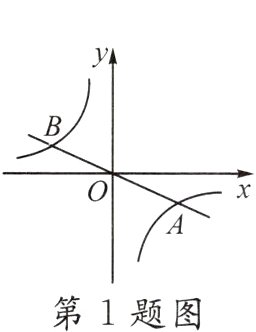
A. $-1\leqslant x<0$或$x\geqslant1$
B. $x\leqslant -1$或$0<x\leqslant1$
C. $x\leqslant -1$或$x\geqslant1$
D. $-1\leqslant x<0$或$0<x\leqslant1$

A. $-1\leqslant x<0$或$x\geqslant1$
B. $x\leqslant -1$或$0<x\leqslant1$
C. $x\leqslant -1$或$x\geqslant1$
D. $-1\leqslant x<0$或$0<x\leqslant1$
答案:
A
2.【几何直观、应用意识、创新意识】(扬州中考)某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)$y$与该校参加竞赛人数$x$的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
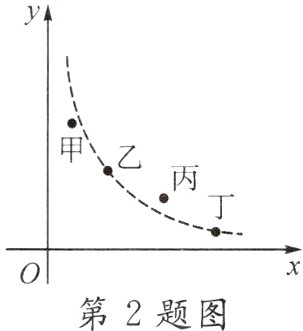
A. 甲
B. 乙
C. 丙
D. 丁

A. 甲
B. 乙
C. 丙
D. 丁
答案:
C
3.【空间观念、应用意识】(无锡中考)一次函数$y = mx + n$的图象与反比例函数$y = \frac{m}{x}$的图象交于点$A,B$,其中点$A,B$的坐标为$A(-\frac{1}{m},-2m),B(m,1)$,则$\triangle OAB$的面积是( )
A. 3
B. $\frac{13}{4}$
C. $\frac{7}{2}$
D. $\frac{15}{4}$
A. 3
B. $\frac{13}{4}$
C. $\frac{7}{2}$
D. $\frac{15}{4}$
答案:
D
4.【应用意识、创新意识】一元二次方程$x^2 - 6x + m = 0$有两个相等的实数根,点$A(x_1,y_1),B(x_2,y_2)$是反比例函数$y = \frac{m}{x}$上的两个点,若$x_1 < x_2 < 0$,则$y_1$______$y_2$(填“<”“>”或“=”).
答案:
>
5.【跨学科融合】【模型观念、应用意识】如图,小明想要用撬棍撬动一块大石头,已知阻力为1600 N,阻力臂长为0.5 m. 设动力为$y$(N),动力臂长为$x$(m).(杠杆平衡时,动力×动力臂 = 阻力×阻力臂,图中撬棍本身所受的重力略去不计)
(1)求$y$关于$x$的函数表达式;
(2)当动力臂长为2 m时,撬动石头至少需要多大的力?
(3)小明若想使动力不超过300 N,在动力臂最大为2.5 m的条件下,他能否撬动这块石头?请说明理由.
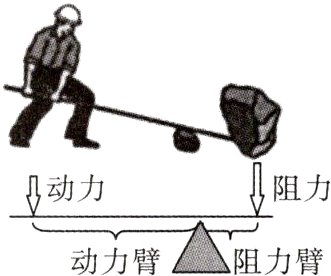
(1)求$y$关于$x$的函数表达式;
(2)当动力臂长为2 m时,撬动石头至少需要多大的力?
(3)小明若想使动力不超过300 N,在动力臂最大为2.5 m的条件下,他能否撬动这块石头?请说明理由.

答案:
解:
(1) 由题意,可得$xy = 1600×0.5$,则$y=\frac{800}{x}$,即$y$关于$x$的函数表达式为$y = \frac{800}{x}(x>0)$。
(2) 在$y=\frac{800}{x}$中,当$x = 2$时,$y=\frac{800}{2}=400$。
∴当动力臂长为$2\ m$时,撬动石头至少需要$400\ N$的力。
(3) 他不能撬动这块石头。理由如下:
在$y=\frac{800}{x}$中,当$0<x\leqslant2.5$时,$0<\frac{800}{y}\leqslant2.5$。解得$y\geqslant320$。$\because320>300$,$\therefore$他不能撬动这块石头。
(1) 由题意,可得$xy = 1600×0.5$,则$y=\frac{800}{x}$,即$y$关于$x$的函数表达式为$y = \frac{800}{x}(x>0)$。
(2) 在$y=\frac{800}{x}$中,当$x = 2$时,$y=\frac{800}{2}=400$。
∴当动力臂长为$2\ m$时,撬动石头至少需要$400\ N$的力。
(3) 他不能撬动这块石头。理由如下:
在$y=\frac{800}{x}$中,当$0<x\leqslant2.5$时,$0<\frac{800}{y}\leqslant2.5$。解得$y\geqslant320$。$\because320>300$,$\therefore$他不能撬动这块石头。
6.【阅读理解,新定义】(遂宁中考)在平面直角坐标系中,如果一个点的横坐标与纵坐标互为相反数,则称该点为“黎点”. 例如$(-1,1),(2022,-2022)$都是“黎点”.
(1)求双曲线$y = -\frac{9}{x}$上的“黎点”;
(2)若抛物线$y = ax^2 - 7x + c$($a,c$为常数)上有且只有一个“黎点”,当$a > 1$时,求$c$的取值范围.
(1)求双曲线$y = -\frac{9}{x}$上的“黎点”;
(2)若抛物线$y = ax^2 - 7x + c$($a,c$为常数)上有且只有一个“黎点”,当$a > 1$时,求$c$的取值范围.
答案:
解:
(1) 设双曲线$y=\frac{-9}{x}$上的“黎点”为$(m,-m)$,则有$-m=\frac{-9}{m}$。解得$m=\pm3$。
经检验,$m = \pm3$是分式方程的解。
∴双曲线$y=\frac{-9}{x}$上的“黎点”为$(3,-3)$或$(-3,3)$。
(2) $\because$抛物线$y = ax^{2}-7x + c$($a$,$c$为常数)上有且只有一个“黎点”,
$\therefore$方程$ax^{2}-7x + c=-x$有且只有一个根,
即$ax^{2}-6x + c = 0$有且只有一个根,
$\therefore\Delta = 36-4ac = 0$,$\therefore ac = 9$。$\therefore a=\frac{9}{c}$。
$\because a>1$,$\therefore0<c<9$。
(1) 设双曲线$y=\frac{-9}{x}$上的“黎点”为$(m,-m)$,则有$-m=\frac{-9}{m}$。解得$m=\pm3$。
经检验,$m = \pm3$是分式方程的解。
∴双曲线$y=\frac{-9}{x}$上的“黎点”为$(3,-3)$或$(-3,3)$。
(2) $\because$抛物线$y = ax^{2}-7x + c$($a$,$c$为常数)上有且只有一个“黎点”,
$\therefore$方程$ax^{2}-7x + c=-x$有且只有一个根,
即$ax^{2}-6x + c = 0$有且只有一个根,
$\therefore\Delta = 36-4ac = 0$,$\therefore ac = 9$。$\therefore a=\frac{9}{c}$。
$\because a>1$,$\therefore0<c<9$。
查看更多完整答案,请扫码查看


