《2025年畅行课堂九年级数学下册人教版山西专版》

7.(2024·周口市郸城县四模改编)开封铁塔(又称开宝寺塔)始建于公元1049年(北宋皇祐元年)，素有“天下第一塔”之称，是国家重点保护文物之一.1957年6月11日开始动工修复开封铁塔，到10月底全部修复竣工，同时还安装了104个铁铸风铃，增装了洞门铁栏和避雷针，千年宝塔以崭新的面貌展现在世人面前.如图，周末，某中学九年级课外兴趣小组在老师的指导下测量铁塔的高度，他们先在铁塔一侧的水平面上一个台阶的底部A处测得塔顶P点的仰角∠1=45°，然后走上台阶顶部B处，测得塔顶P点的仰角∠2=38.8°.若台阶的高BC=3米，台阶斜坡AB的坡度为3:10，则铁塔的高度PE=______米.(点C，A，E在一条直线上，结果保留整数，参考数据：tan38.8°≈0.8)

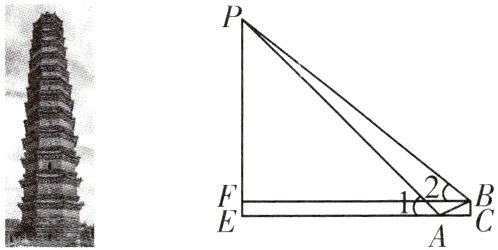
答案： 55

8.(2024·广安)风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在某地安装了一批风力发电机，如图(1)，某校实践活动小组对其中一架风力发电机的塔杆高度进行了测量，图(2)为测量示意图(点A，B，C，D均在同一平面内，AB⊥BC).已知斜坡CD长为20米，斜坡CD的坡角为60°，在斜坡顶部D处测得风力发电机塔杆顶端A点的仰角为20°，坡底与塔杆底的距离BC=30米，求该风力发电机塔杆AB的高度.(结果精确到个位；参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，$\sqrt{3}$≈1.73)

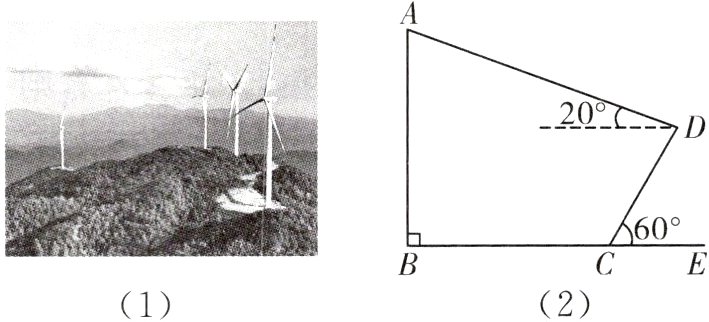
答案：
解:如图，过点D作$DF\perp AB$于点F，作$DH\perp BE$于点H.
　　　　　
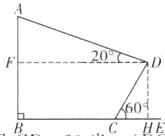
由题意，得$CD = 20$米，$\angle DCH = 60^{\circ}$
在$Rt\triangle DHC$中
$\because\cos60^{\circ}=\frac{CH}{CD},\sin60^{\circ}=\frac{DH}{CD}$
$\therefore CH = CD\cdot\cos60^{\circ}=10(米)$
$\therefore DH = CD\cdot\sin60^{\circ}=10\sqrt{3}米\approx17.3(米)$
$\because\angle DFB=\angle B=\angle DHB = 90^{\circ}$
$\therefore$四边形DFBH为矩形
$\therefore BH = FD,BF = DH$
$\because BH = BC + CH = 30 + 10 = 40(米)$
$\therefore FD = 40$米
在$Rt\triangle AFD$中，$\because\tan20^{\circ}=\frac{AF}{FD}$
$\therefore AF = FD\cdot\tan20^{\circ}\approx40\times0.36 = 14.4(米)$
$\therefore AB = AF + BF = 14.4 + 17.3 = 31.7(米)\approx32(米)$
答:该风力发电机塔杆AB的高度约为32米.