《2025年畅行课堂九年级数学下册人教版山西专版》

8.(2024·牡丹江)矩形$OBAC$在平面直角坐标系中的位置如图所示，反比例函数$y=\frac{k}{x}$的图象与$AB$边交于点$D$，与$AC$边交于点$F$，与$OA$交于点$E$，$OE = 2AE$，若四边形$ODAF$的面积为2，则$k$的值是（ ）
　　　　　
A. $\frac{2}{5}$
B. $\frac{3}{5}$
C. $\frac{4}{5}$
D. $\frac{8}{5}$

答案： D

9.(2024·绥化)如图，已知点$A(-7,0)$，$B(x,10)$，$C(-17,y)$，在平行四边形$ABCO$中，它的对角线$OB$与反比例函数$y=\frac{k}{x}$（$k\ne0$）的图象相交于点$D$，且$OD:OB = 1:4$，则$k=$____.
　　　　　

答案： −15

10.(2023·陕西)如图，在矩形$OABC$和正方形$CDEF$中，点$A$在$y$轴正半轴上，点$C$，$F$均在$x$轴正半轴上，点$D$在边$BC$上，$BC = 2CD$，$AB = 3$.若点$B$，$E$在同一个反比例函数的图象上，则这个反比例函数的表达式是____.
　　　　　　　

答案： y=$\frac{18}{x}$

11.如图，$Rt\triangle ABC$的一个顶点$B$在原点，$BC$在$y$轴上，直角边$AC = 1$，$BC = 2$，把$Rt\triangle ABC$绕点$B$逆时针旋转$90^{\circ}$，顶点$A$的对应点为$A'$.若反比例函数$y=\frac{m}{x}$的图象经过点$A'$，则$m$的值为（ ）
　　　　　　　
A. -2
B. -1
C. 1
D. 2

答案： A

12.(毕节中考)如图，在平面直角坐标系中，一次函数$y=-4x + 4$的图象与$x$轴，$y$轴分别交于$A$，$B$两点.正方形$ABCD$的顶点$C$，$D$在第一象限，顶点$D$在反比例函数$y=\frac{k}{x}$（$k\ne0$）的图象上.若正方形$ABCD$向左平移$n$个单位长度后，顶点$C$恰好落在反比例函数的图象上，则$n$的值是____.
　　　　　　　

答案： 3

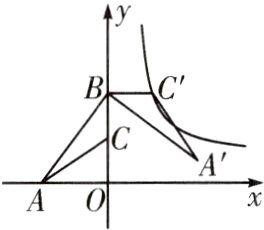
13.(2023·湘潭)如图，点$A$的坐标是(-3,0)，点$B$的坐标是(0,4)，点$C$为$OB$中点.将$\triangle ABC$绕着点$B$逆时针旋转$90^{\circ}$得到$\triangle A'BC'$.
(1)反比例函数$y=\frac{k}{x}$的图象经过点$C'$，求该反比例函数的表达式；
(2)一次函数图象经过$A$，$A'$两点，求该一次函数的表达式.
　　　　　　　　　　　　

答案：
解:
(1)
∵点A的坐标是(−3,0),点B的坐标是(0,4),点C为OB中点，
∴OA=3,OB=4,
∴BC=2,
　将△ABC绕着点B逆时针旋转90°得到△A'BC',
∴点C'的坐标为(2,4).
∵反比例函数y=$\frac{k}{x}$的图象经过点C',
　
∴k=2×4=8,
　
∴该反比例函数的表达式为y=$\frac{8}{x}$.
(2)如图,过点A'作A'H⊥y轴于点H.
　　　　　　
　
∵∠AOB=∠A'HB=∠ABA'=90°,
∴∠ABO+∠A'BH=90°,∠ABO+∠BAO=90°,
　
∴∠BAO=∠A'BH,
∵BA=A'B,
∴△AOB≌△BHA'(AAS),
　
∴OA=BH,OB=A'H,
　
∵OA=3,OB=4,
∴BH=OA=3,A'H=OB=4,
∴OH=1,
∴A'(4,1).
设过A,A'两点的一次函数的表达式为y=ax+b,把A(−3,0),A'(4,1)代入,得$\begin{cases}-3a + b = 0 \\ 4a + b = 1\end{cases}$,解得$\begin{cases}a = \frac{1}{7} \\ b = \frac{3}{7}\end{cases}$.
∴该一次函数的表达式为y=$\frac{1}{7}$x+$\frac{3}{7}$.