《2025年畅行课堂九年级数学下册人教版山西专版》

10.如果两个相似三角形的相似比为3∶5，周长的差为4 cm，那么较大三角形的周长为______cm.

答案： 10

11.【教材九下P43习题T12变式】(训练角度：相似三角形的判定与性质)如图，在△ABC中，点D，E分别在边AB和AC上，且DE//BC.
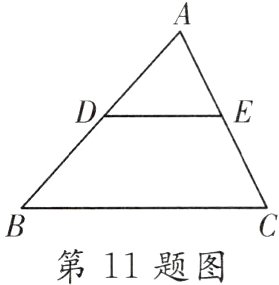
(1)若AD∶DB = 1∶1，则S△ADE∶S四边形DBCE = __________；
(2)若S△ADE = S四边形DBCE，则AD∶DB = ________.
　

答案：
(1)$\frac{1}{3}$　
(2)$\sqrt{2}+1$

12.如图，在△ABC中，点D，E分别在AB，AC上，AF平分∠BAC交DE于点G.若AE = 3，EC = 1，AD = 2，BD = 4，则AG∶AF的值为__________.
　

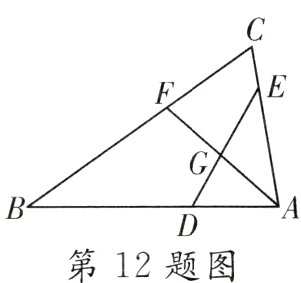
答案： $\frac{1}{2}$

13.(2022·杭州)如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，连接DE，EF.已知四边形BFED是平行四边形，$\frac{DE}{BC}$ = $\frac{1}{4}$.
(1)若AB = 8，求线段AD的长；
(2)若△ADE的面积为1，求□BFED的面积.
　　　　　　　　　　　

答案： 解:
(1)
∵四边形BFED是平行四边形，
∴DE//BF.
∴DE//BC.
∴△ADE∽△ABC.
∴$\frac{AD}{AB}=\frac{DE}{BC}=\frac{1}{4}$.
∵AB = 8，
∴AD = 2.
(2)
∵△ADE∽△ABC，
∴$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=(\frac{DE}{BC})^2=(\frac{1}{4})^2=\frac{1}{16}$.
∵$S_{\triangle ADE}=1$，
∴$S_{\triangle ABC}=16$.
∵$\frac{AD}{AB}=\frac{1}{4}$，
∴$\frac{BD}{AB}=\frac{3}{4}$.
∵四边形BFED是平行四边形，
∴EF//AB，EF = BD.
∴△EFC∽△ABC，$\frac{EF}{AB}=\frac{3}{4}$.
∴$\frac{S_{\triangle EFC}}{S_{\triangle ABC}}=(\frac{3}{4})^2=\frac{9}{16}$.
∴$S_{\triangle EFC}=9$.
∴$S_{BFED}=16 - 9 - 1 = 6$.

14.一块直角三角形木板的面积为1.5 m²，其中一条直角边AB为1.5 m，怎样才能把它加工成一个无拼接且面积最大的正方形桌面？甲、乙两位木匠的加工方法如图所示，请你用学过的知识说明哪位木匠的方法符合要求(加工损耗不计，计算结果中的分数可保留).
　　　

答案：
解:由AB = 1.5 m，$S_{\triangle ABC}=1.5 m^2$，可得BC = 2 m.
甲:如图,过点B作BH⊥AC于点H,交DE于点P.

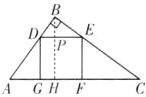
∵AB = 1.5 m，BC = 2 m，
∴$AC=\sqrt{AB^{2}+BC^{2}}=2.5 m$.
由$S_{\triangle ABC}=\frac{1}{2}AC\cdot BH=\frac{1}{2}AB\cdot BC$，得$BH=\frac{AB\cdot BC}{AC}=1.2(m)$.
设甲设计的正方形桌面的边长为x m.
∵DE//AC，
∴Rt△BDE∽Rt△BAC.
∴$\frac{BP}{BH}=\frac{DE}{AC}$，即$\frac{1.2 - x}{1.2}=\frac{x}{2.5}$，
解得$x=\frac{30}{37}$.
∴甲设计的正方形桌面的边长为$\frac{30}{37}$m.
乙:设乙设计的正方形桌面的边长为y m，
由DE//AB，得Rt△CDE∽Rt△CBA.
∴$\frac{DE}{BA}=\frac{CD}{CB}$，即$\frac{y}{1.5}=\frac{2 - y}{2}$，
解得$y=\frac{6}{7}$.
∴乙设计的正方形桌面的边长为$\frac{6}{7}$m.
∵$0＜\frac{30}{37}＜\frac{6}{7}$，
∴$(\frac{30}{37})^2＜(\frac{6}{7})^2$，
即$S_{正方形甲}＜S_{正方形乙}$.
∴乙木匠的方法符合要求.