《2025年畅行课堂九年级数学下册人教版山西专版》

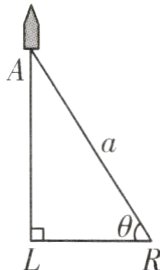
1.(2024·长春)如图，2024年5月29日16时12分，“长春净月一号”卫星搭乘谷神星一号火箭在黄海海域成功发射。当火箭上升到点A时，位于海平面R处的雷达测得点R到点A的距离为a千米，仰角为θ，则此时火箭距海平面的高度AL为（ ）
A. $a\sin\theta$千米
B. $\frac{a}{\sin\theta}$千米
C. $a\cos\theta$千米
D. $\frac{a}{\cos\theta}$千米
　　　　　　　

答案： A

2.(2024·郑州模拟)一配电房示意图如图所示，它是一个轴对称图形。已知BC = 6 m，∠ABC = α，则房顶A离地面EF的高度为（ ）
A. $(4 + 3\sin\alpha)$ m
B. $(4 + 3\tan\alpha)$ m
C. $(4+\frac{3}{\sin\alpha})$ m
D. $(4+\frac{3}{\tan\alpha})$ m
　　 　　

答案： B

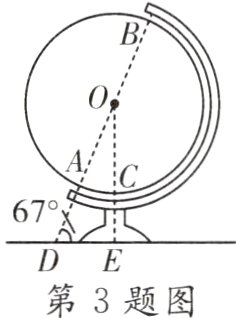
3.如图，点A，B分别为地球仪的南、北极点，直线AB与放置地球仪的平面相交于点D，所成的角度约为67°，半径OA所在的直线与放置平面垂直，垂足为E。若DE = 15 cm，AD = 14 cm，则半径OA的长为________ cm。（结果精确到0.1 cm，参考数据：$\sin 67^{\circ}\approx0.92$，$\cos 67^{\circ}\approx0.39$，$\tan 67^{\circ}\approx2.36$）

答案： 24.5

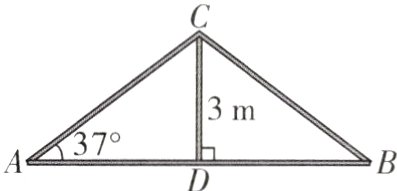
4.(2023·广西)如图，焊接一个钢架，包括底角为37°的等腰三角形外框和3 m高的支柱，则共需钢材约______ m（结果取整数）。（参考数据：$\sin37^{\circ}\approx0.60$，$\cos37^{\circ}\approx0.80$，$\tan37^{\circ}\approx0.75$）
　　　　　　　　　

答案： 21

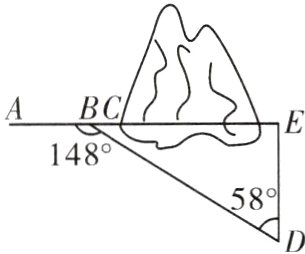
5.(2024·洛阳市汝阳县一模改编)如图，沿AC的方向开山修路，为了加快速度，要在小山的另一边同时施工，从AC上取一点B，取∠ABD = 148°，已知BD = 600米，∠D = 58°，点A，C，E在同一直线上，那么开挖点E离点D的距离是多少米？
　　　

答案： 解：
∵∠ABD = 148°，
∴∠DBE = 180° - ∠ABD = 180° - 148° = 32°，
∴∠E = 180° - 32° - 58° = 90°，
∴△BDE是直角三角形.
∵BD = 600米，
∴DE = BD·cos58° = 600cos58°米.
答：开挖点E离点D的距离是600cos58°米.

6.(2024·南通)社团活动课上，九年级学习小组测量学校旗杆的高度。如图，他们在B处测得旗杆顶部A的仰角为60°，BC = 6 m，则旗杆AC的高度为________ m。
　　　　　　　 　　　　

答案： 6√3

7.(2024·绥化)如图，用热气球的探测器测一栋楼的高度，从热气球上的点A测得该楼顶部点C的仰角为60°，测得底部点B的俯角为45°，点A与楼BC的水平距离AD = 50 m，则这栋楼的高度为 ____________ m（结果保留根号）。

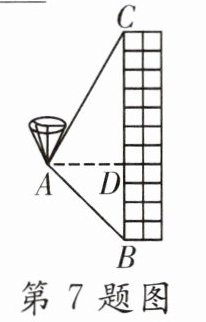
答案： (50 + 50√3)

8.【真实问题情境】某老年活动中心欲在一房前3 m高的前墙(AB)上安装一遮阳篷BC，使正午时刻房前能有2 m宽的阴影处(AD)以供纳凉。假设此地某日正午时刻太阳光与水平地面的夹角为63.4°，遮阳篷BC与水平面的夹角为10°。侧面示意图如图所示，则此遮阳篷BC的长度为________ m。（结果精确到0.1 m）
（参考数据：$\sin10^{\circ}\approx0.17$，$\cos10^{\circ}\approx0.98$，$\tan10^{\circ}\approx0.18$；$\sin63.4^{\circ}\approx0.89$，$\cos63.4^{\circ}\approx0.45$，$\tan63.4^{\circ}\approx2.00$）
　　　　　　

答案： 3.4

9.(2024·呼伦贝尔)综合实践活动中，数学兴趣小组利用无人机测量大楼的高度。如图，无人机在离地面40米的D处，测得操控者A的俯角为30°，测得楼BC楼顶C处的俯角为45°，又经过人工测量得到操控者A和大楼BC之间的水平距离是80米，则楼BC的高度是多少米？（点A，B，C，D都在同一平面内，参考数据：$\sqrt{3}\approx1.7$）
　　　　

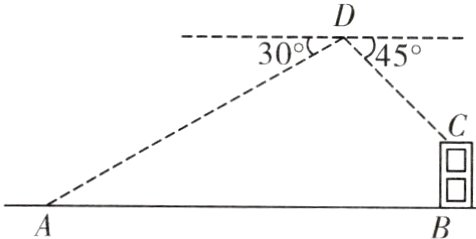
答案：
解：如图，过点D作DE⊥AB于点E，过点C作CF⊥DE于点F，

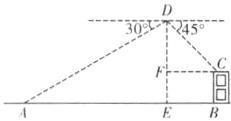
则四边形BCFE是矩形.
由题意，得AB = 80米，DE = 40米，∠ADE = 90° - 30° = 60°，∠CDF = 90° - 45° = 45°.
在Rt△AED中，
∵∠AED = 90°，
∴tan∠ADE = $\frac{AE}{DE}$ = tan60° = √3，
∴AE = √3DE = 40√3米，
∴BE = AB - AE = (80 - 40√3)米.
∵四边形BCFE是矩形，
∴CF = BE = (80 - 40√3)米.
在Rt△DFC中，
∵∠DFC = 90°，∠CDF = ∠DCF = 45°，
∴DF = CF = (80 - 40√3)米，
∴BC = EF = DE - DF = 40 - 80 + 40√3 ≈ 28(米).
答：楼BC高度约是28米.