《2025年畅行课堂九年级数学下册人教版山西专版》

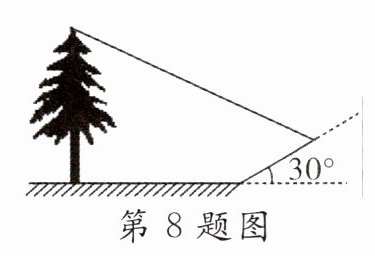
8.小明想测量一棵树的高度，他发现树的影子恰好落在地面和斜坡上，如图，此时测得地面上的影长为8 m，坡面上的影长为4 m.已知斜坡的坡角为30°，同一时刻，一根长为1 m，且垂直于地面放置的标杆在地面上的影长为2 m，则斜坡上树影顶端到地面的距离为____m，树的高度为__________m.（结果保留根号）
　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　

答案： $2(6 + \sqrt{3})$

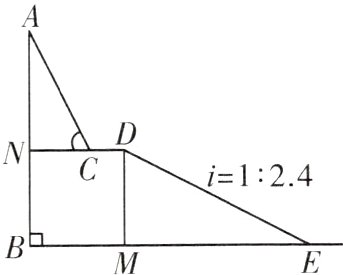
9.(2024·南阳市镇平县模拟)2024年春节前夕，哈尔滨旅游市场的火热带动了全国“冰雪旅游”的繁荣，某地准备依山建设一个滑雪场带动本地旅游的发展.如图，小山AB的山腰CN上有一个平台CD长为45 m，从点C看山顶A的仰角为63°，山坡DE的坡度为i=1∶2.4，该地准备利用斜坡DE建设一个滑雪场，且DE的长度为390 m，若点D到地面BE的垂线段与BN构成的四边形恰好为正方形时，且图中各点均在一个平面内，求小山AB的高度.（精确到整数，参考数据：sin63°≈0.89，cos63°≈0.45，tan63°≈1.96）
　　　　　　　　　　

答案： 解：
∵山坡DE的坡度为$i = 1:2.4$，
∴$\frac{DM}{ME}=\frac{1}{2.4}=\frac{5}{12}$.
设DM = 5x m，则ME = 12x m，
在Rt△DME中，由勾股定理，得$DM^{2}+ME^{2}=DE^{2}$，即$(5x)^{2}+(12x)^{2}=390^{2}$，
解得x = 30或x = -30(舍去)，
∴DM = 5×30 = 150(m).
∵四边形NBMD为正方形，
∴BN = DM = DN = 150 m，
∴CN = DN - CD = 150 - 45 = 105(m).
在Rt△ANC中，
∵∠ACN = 63°，
∴AN = NC·tan63°≈205.8 m，
∴AB = AN + BN = 355.8≈356(m).
答：小山AB的高度约为356 m.

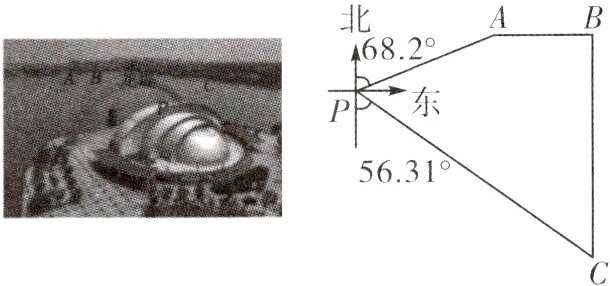
10.(2023·聊城)东昌湖西岸的明珠大剧院，隔湖与远处的角楼、城门楼、龙堤、南关桥等景观遥相呼应.如图所示，城门楼B在角楼A的正东方向520 m处，南关桥C在城门楼B的正南方向1 200 m处.在明珠大剧院P测得角楼A在北偏东68.2°方向，南关桥C在南偏东56.31°方向（点A，B，C，P四点在同一平面内），求明珠大剧院到龙堤BC的距离.（结果精确到1 m）（参考数据：sin68.2°≈0.928，cos68.2°≈0.371，tan68.2°≈2.50，sin56.31°≈0.832，cos56.31°≈0.555，tan56.31°≈1.50）
　　　

答案：
解：如图，过点P作PE⊥BC于点E，过点A作AD⊥PE于点D，
则四边形ADEB是矩形，
∴DE = AB = 520 m.
设PD = x m，则PE = PD + DE = (x + 520)m.
在Rt△APD中，
∵∠PAD = 68.2°，
∴$AD=\frac{PD}{\tan68.2^{\circ}}\approx\frac{x}{2.5}=\frac{2}{5}x$ m，
∴BE = AD = $\frac{2}{5}x$ m，
∴$CE = BC - BE=(1200-\frac{2}{5}x)$ m.
在Rt△PCE中，$\tan C=\tan56.31^{\circ}=\frac{PE}{CE}$，
∴$\frac{x + 520}{1200-\frac{2}{5}x}\approx1.5$，解得x≈800，即PD≈800 m，
∴PE = PD + DE≈800 + 520 = 1320(m).
答：明珠大剧院到龙堤BC的距离约为1320 m.