2025年畅行课堂九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年畅行课堂九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
10.(2024·资阳)第14届国际数学教育大会(ICME - 14)会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图2所示的“弦图”是由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF∶AH = 1∶3,则sin∠ABE = ( )

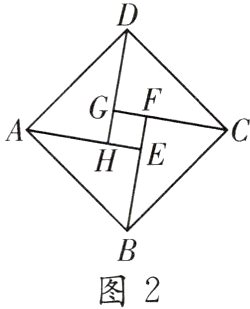
A.$\frac{\sqrt{5}}{5}$
B.$\frac{3}{5}$
C.$\frac{4}{5}$
D.$\frac{2\sqrt{5}}{5}$


A.$\frac{\sqrt{5}}{5}$
B.$\frac{3}{5}$
C.$\frac{4}{5}$
D.$\frac{2\sqrt{5}}{5}$
答案:
C
11.(宁波中考)如图,在△ABC中,∠B = 45°,∠C = 60°,AD⊥BC于点D,BD = $\sqrt{3}$.若E,F分别为AB,BC的中点,则EF的长为 ( )
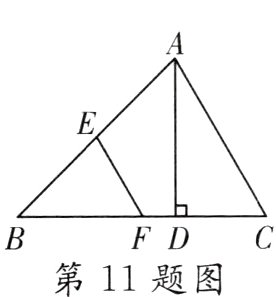
A.$\frac{\sqrt{3}}{3}$
B.$\frac{\sqrt{3}}{2}$
C.1
D.$\frac{\sqrt{6}}{2}$

A.$\frac{\sqrt{3}}{3}$
B.$\frac{\sqrt{3}}{2}$
C.1
D.$\frac{\sqrt{6}}{2}$
答案:
C
12.(2022·凉山州)如图,⊙O的直径AB经过弦CD的中点H.若cos∠CDB = $\frac{4}{5}$,BD = 5,则⊙O的半径为 _________.
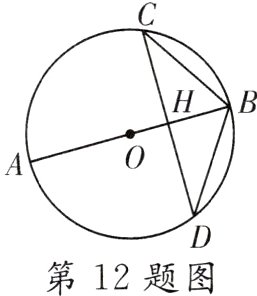

答案:
$\frac{25}{6}$
13.(2024·浙江)如图,在△ABC中,AD⊥BC,AE是BC边上的中线,AB = 10,AD = 6,tan∠ACB = 1.
(1)求BC的长;
(2)求sin∠DAE的值.
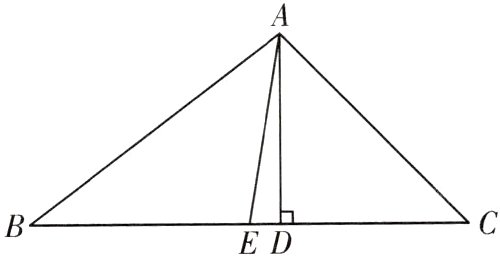
(1)求BC的长;
(2)求sin∠DAE的值.

答案:
解:
(1)
∵AD⊥BC,AB=10,AD=6,
∴BD=$\sqrt{AB^{2}-AD^{2}}$=$\sqrt{10^{2}-6^{2}}$=8.
∵tan∠ACB=1,
∴CD=AD=6,
∴BC=BD+CD=8+6=14.
(2)
∵AE是BC边上的中线,
∴CE=$\frac{1}{2}$BC=7,
∴DE=CE−CD=7−6=1.
∵AD⊥BC,
∴AE=$\sqrt{AD^{2}+DE^{2}}$=$\sqrt{6^{2}+1^{2}}$=$\sqrt{37}$,
∴sin∠DAE=$\frac{DE}{AE}$=$\frac{1}{\sqrt{37}}$=$\frac{\sqrt{37}}{37}$.
(1)
∵AD⊥BC,AB=10,AD=6,
∴BD=$\sqrt{AB^{2}-AD^{2}}$=$\sqrt{10^{2}-6^{2}}$=8.
∵tan∠ACB=1,
∴CD=AD=6,
∴BC=BD+CD=8+6=14.
(2)
∵AE是BC边上的中线,
∴CE=$\frac{1}{2}$BC=7,
∴DE=CE−CD=7−6=1.
∵AD⊥BC,
∴AE=$\sqrt{AD^{2}+DE^{2}}$=$\sqrt{6^{2}+1^{2}}$=$\sqrt{37}$,
∴sin∠DAE=$\frac{DE}{AE}$=$\frac{1}{\sqrt{37}}$=$\frac{\sqrt{37}}{37}$.
14.如图,⊙O的半径为R,在其内接锐角三角形ABC中,∠A,∠B,∠C所对边的长分别是a,b,c.
(1)求证:$\frac{a}{sinA}$ = $\frac{b}{sinB}$ = $\frac{c}{sinC}$ = 2R;
(2)若∠A = 60°,∠C = 45°,BC = 4$\sqrt{3}$,利用(1)的结论求AB的长和sinB的值.
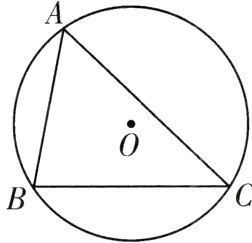
(1)求证:$\frac{a}{sinA}$ = $\frac{b}{sinB}$ = $\frac{c}{sinC}$ = 2R;
(2)若∠A = 60°,∠C = 45°,BC = 4$\sqrt{3}$,利用(1)的结论求AB的长和sinB的值.

答案:
(1)证明:如图,连接BO并延长交⊙O 于点E,连接CE,则∠BCE=90°,∠E =∠A,
∴sinA=sinE=$\frac{BC}{BE}$=$\frac{a}{2R}$
∴$\frac{a}{sinA}$=2R.
同理,得$\frac{b}{sinB}$=2R,$\frac{c}{sinC}$=2R,
∴$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R.
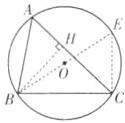
(2)解:由
(1),得$\frac{AB}{sin\angle ACB}$=$\frac{BC}{sinA}$=2R,
即$\frac{AB}{sin45°}$=$\frac{4\sqrt{3}}{sin60°}$=2R,
∴AB=$\frac{4\sqrt{3}\times\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=4$\sqrt{2}$,2R=$\frac{4\sqrt{3}}{\frac{\sqrt{3}}{2}}$=8.
如图,过点B作BH⊥AC于点H,则∠AHB=∠BHC=90°,
∴AH=AB·cos60°=4$\sqrt{2}$×$\frac{1}{2}$=2$\sqrt{2}$,
CH=$\frac{\sqrt{2}}{2}$BC=2$\sqrt{6}$,
∴AC=AH+CH=2($\sqrt{2}$+$\sqrt{6}$),
∴sin∠ABC=$\frac{AC}{2R}$=$\frac{2(\sqrt{2}+\sqrt{6})}{8}$=$\frac{\sqrt{2}+\sqrt{6}}{4}$.
∴AB的长为4$\sqrt{2}$,sinB的值为$\frac{\sqrt{2}+\sqrt{6}}{4}$
(1)证明:如图,连接BO并延长交⊙O 于点E,连接CE,则∠BCE=90°,∠E =∠A,
∴sinA=sinE=$\frac{BC}{BE}$=$\frac{a}{2R}$
∴$\frac{a}{sinA}$=2R.
同理,得$\frac{b}{sinB}$=2R,$\frac{c}{sinC}$=2R,
∴$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R.

(2)解:由
(1),得$\frac{AB}{sin\angle ACB}$=$\frac{BC}{sinA}$=2R,
即$\frac{AB}{sin45°}$=$\frac{4\sqrt{3}}{sin60°}$=2R,
∴AB=$\frac{4\sqrt{3}\times\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=4$\sqrt{2}$,2R=$\frac{4\sqrt{3}}{\frac{\sqrt{3}}{2}}$=8.
如图,过点B作BH⊥AC于点H,则∠AHB=∠BHC=90°,
∴AH=AB·cos60°=4$\sqrt{2}$×$\frac{1}{2}$=2$\sqrt{2}$,
CH=$\frac{\sqrt{2}}{2}$BC=2$\sqrt{6}$,
∴AC=AH+CH=2($\sqrt{2}$+$\sqrt{6}$),
∴sin∠ABC=$\frac{AC}{2R}$=$\frac{2(\sqrt{2}+\sqrt{6})}{8}$=$\frac{\sqrt{2}+\sqrt{6}}{4}$.
∴AB的长为4$\sqrt{2}$,sinB的值为$\frac{\sqrt{2}+\sqrt{6}}{4}$
查看更多完整答案,请扫码查看


