2025年畅行课堂九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年畅行课堂九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
11. 如图,在△ABC中,AD = DB,∠1 = ∠2.
(1)求证:△ABC∽△EAD;
(2)若$S_{△ABC}∶S_{△EAD}= 9∶4$,BC = 6,求AD的长.
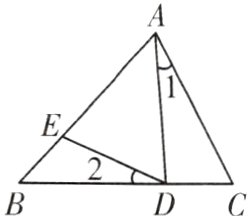
(1)求证:△ABC∽△EAD;
(2)若$S_{△ABC}∶S_{△EAD}= 9∶4$,BC = 6,求AD的长.

答案:
(1)证明:$\because AD = DB$,
$\therefore \angle B=\angle BAD$.
$\because \angle BDA=\angle 1+\angle C=\angle 2+\angle ADE$,
又$\because \angle 1=\angle 2$,$\therefore \angle C=\angle ADE$.
$\therefore \triangle ABC\sim\triangle EAD$.
(2)解:$\because \triangle ABC\sim\triangle EAD$,
$\therefore \frac{S_{\triangle ABC}}{S_{\triangle EAD}} = (\frac{CB}{DA})^2=\frac{9}{4}$.$\therefore \frac{CB}{DA}=\frac{3}{2}$,
即$\frac{6}{DA}=\frac{3}{2}$.
$\therefore AD = 4$.
(1)证明:$\because AD = DB$,
$\therefore \angle B=\angle BAD$.
$\because \angle BDA=\angle 1+\angle C=\angle 2+\angle ADE$,
又$\because \angle 1=\angle 2$,$\therefore \angle C=\angle ADE$.
$\therefore \triangle ABC\sim\triangle EAD$.
(2)解:$\because \triangle ABC\sim\triangle EAD$,
$\therefore \frac{S_{\triangle ABC}}{S_{\triangle EAD}} = (\frac{CB}{DA})^2=\frac{9}{4}$.$\therefore \frac{CB}{DA}=\frac{3}{2}$,
即$\frac{6}{DA}=\frac{3}{2}$.
$\therefore AD = 4$.
12.(2024·广州)如图,点E,F分别在正方形ABCD的边BC,CD上,BE = 3,EC = 6,CF = 2. 求证:△ABE∽△ECF.


答案:
证明:$\because BE = 3$,$EC = 6$,$CF = 2$,
$\therefore BC = 3 + 6 = 9$,
$\because$四边形$ABCD$是正方形,
$\therefore AB = BC = 9$,$\angle B=\angle C = 90^{\circ}$.
$\because \frac{AB}{EC}=\frac{9}{6}=\frac{3}{2}$,$\frac{BE}{CF}=\frac{3}{2}$,
$\therefore \frac{AB}{EC}=\frac{BE}{CF}$,$\therefore \triangle ABE\sim\triangle ECF$.
$\therefore BC = 3 + 6 = 9$,
$\because$四边形$ABCD$是正方形,
$\therefore AB = BC = 9$,$\angle B=\angle C = 90^{\circ}$.
$\because \frac{AB}{EC}=\frac{9}{6}=\frac{3}{2}$,$\frac{BE}{CF}=\frac{3}{2}$,
$\therefore \frac{AB}{EC}=\frac{BE}{CF}$,$\therefore \triangle ABE\sim\triangle ECF$.
13.(毕节中考)如图,在一块斜边长30 cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF∶AC = 1∶3,则这块木板截取正方形CDEF后,剩余部分的面积为 ( )

A. 100 cm²
B. 150 cm²
C. 170 cm²
D. 200 cm²

A. 100 cm²
B. 150 cm²
C. 170 cm²
D. 200 cm²
答案:
A
14.【跨学科融合】如图,点B是一根均匀的木棍OA的中点,如果以O点为支点,在A处需用5 N的力竖直向上拉才能保持木棍不动,根据杠杆原理可求木棍OA所受的重力G的大小是 ( )
A. 5 N
B. 15 N
C. 10 N
D. 20 N

A. 5 N
B. 15 N
C. 10 N
D. 20 N

答案:
C
15. 古希腊数学家泰勒斯曾利用立杆测影的方法,在金字塔影子的顶部直立一根木杆,借助太阳光测量金字塔的高度. 如图,木杆EF长2米,它的影长FD是4米,同一时刻测得OA是268米,则金字塔的高度BO是 ______米.
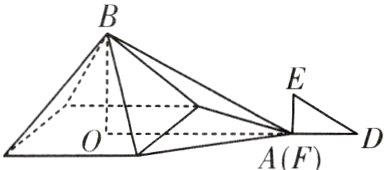

答案:
134
16.(2024·浙江)如图,在平面直角坐标系中,△ABC与△A'B'C'是位似图形,位似中心为点O. 若点A(-3,1)的对应点为A'(-6,2),则点B(-2,4)的对应点B'的坐标为 ( )
A.(-4,8)
B.(8,-4)
C.(-8,4)
D.(4,-8)
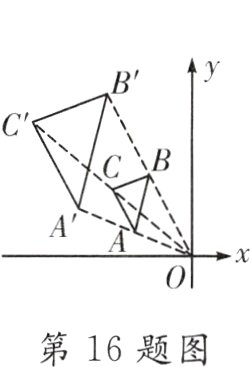
A.(-4,8)
B.(8,-4)
C.(-8,4)
D.(4,-8)

答案:
A
17.(2022·黔西南州)如图,在平面直角坐标系中,△OAB与△OCD位似,位似中心是坐标原点O. 若点A(4,0),点C(2,0),则△OAB与△OCD周长的比值是 ______.


答案:
2
18. 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(4,1),B(2,3),C(1,2).
(1)画出与△ABC关于y轴对称的△A₁B₁C₁;
(2)以原点O为位似中心,在第三象限内画一个△A₂B₂C₂,使它与△ABC的相似比为2∶1,并写出点B₂的坐标.
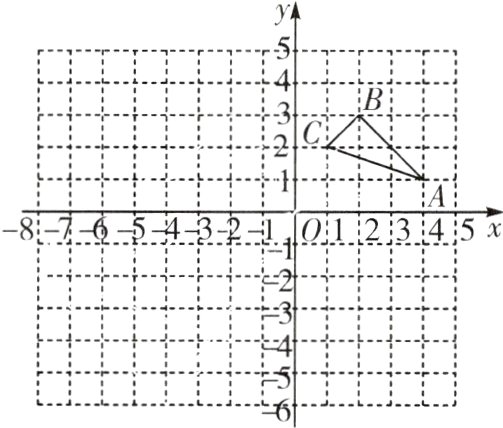
(1)画出与△ABC关于y轴对称的△A₁B₁C₁;
(2)以原点O为位似中心,在第三象限内画一个△A₂B₂C₂,使它与△ABC的相似比为2∶1,并写出点B₂的坐标.

答案:
解:
(1)如图,$\triangle ABC$即为所求,

(2)如图,$\triangle ABC$即为所求,点$B$的坐标为$(-4,-6)$.
解:
(1)如图,$\triangle ABC$即为所求,

(2)如图,$\triangle ABC$即为所求,点$B$的坐标为$(-4,-6)$.
查看更多完整答案,请扫码查看


