2025年畅行课堂九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年畅行课堂九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
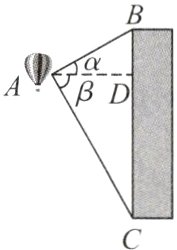
热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?

答案:
解:如图,$\alpha = 30^{\circ},\beta = 60^{\circ},AD = 120$.
$\because\tan\alpha=\frac{BD}{AD},\tan\beta=\frac{CD}{AD}$
$\therefore BD = AD\cdot\tan\alpha = 120\times\tan30^{\circ}=120\times\frac{\sqrt{3}}{3}=40\sqrt{3}(m)$
$CD = AD\cdot\tan\beta = 120\times\tan60^{\circ}=120\times\sqrt{3}=120\sqrt{3}(m)$
$\therefore BC = BD + CD = 40\sqrt{3}+120\sqrt{3}=160\sqrt{3}\approx277(m)$
因此,这栋楼高约为277m.
$\because\tan\alpha=\frac{BD}{AD},\tan\beta=\frac{CD}{AD}$
$\therefore BD = AD\cdot\tan\alpha = 120\times\tan30^{\circ}=120\times\frac{\sqrt{3}}{3}=40\sqrt{3}(m)$
$CD = AD\cdot\tan\beta = 120\times\tan60^{\circ}=120\times\sqrt{3}=120\sqrt{3}(m)$
$\therefore BC = BD + CD = 40\sqrt{3}+120\sqrt{3}=160\sqrt{3}\approx277(m)$
因此,这栋楼高约为277m.
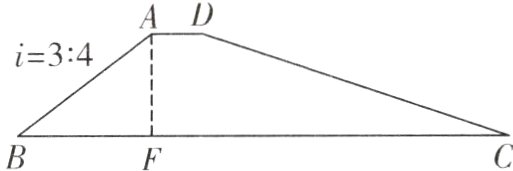
1.(2023·天门改编)为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形ABCD,斜面坡度i=3:4是指坡面的铅直高度AF与水平宽度BF的比.已知斜坡CD长度为20米,∠C=18°,求斜坡AB的长.(结果精确到0.1米)(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)

答案:
解:如图,过点D作$DE\perp BC$,垂足分别为E.
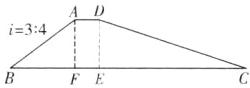
由题意,得$\angle AFB=\angle DEC = 90^{\circ},DE = AF$.
$\because$斜面AB的坡度$i = 3:4$
$\therefore\frac{AF}{BF}=\frac{3}{4}$
设$AF = 3x$米,则$BF = 4x$米.
在$Rt\triangle ABF$中,$AB=\sqrt{AF^{2}+BF^{2}}=\sqrt{(3x)^{2}+(4x)^{2}} = 5x(米)$
在$Rt\triangle DEC$中,$\angle C = 18^{\circ}$,$CD = 20$米
$\therefore DE = CD\cdot\sin18^{\circ}\approx20\times0.31 = 6.2(米)$
$\therefore AF = DE = 6.2$米
即$3x = 6.2$,解得$x=\frac{31}{15}$
$\therefore AB = 5x\approx10.3(米)$
答:斜坡AB的长约为10.3米.
解:如图,过点D作$DE\perp BC$,垂足分别为E.

由题意,得$\angle AFB=\angle DEC = 90^{\circ},DE = AF$.
$\because$斜面AB的坡度$i = 3:4$
$\therefore\frac{AF}{BF}=\frac{3}{4}$
设$AF = 3x$米,则$BF = 4x$米.
在$Rt\triangle ABF$中,$AB=\sqrt{AF^{2}+BF^{2}}=\sqrt{(3x)^{2}+(4x)^{2}} = 5x(米)$
在$Rt\triangle DEC$中,$\angle C = 18^{\circ}$,$CD = 20$米
$\therefore DE = CD\cdot\sin18^{\circ}\approx20\times0.31 = 6.2(米)$
$\therefore AF = DE = 6.2$米
即$3x = 6.2$,解得$x=\frac{31}{15}$
$\therefore AB = 5x\approx10.3(米)$
答:斜坡AB的长约为10.3米.
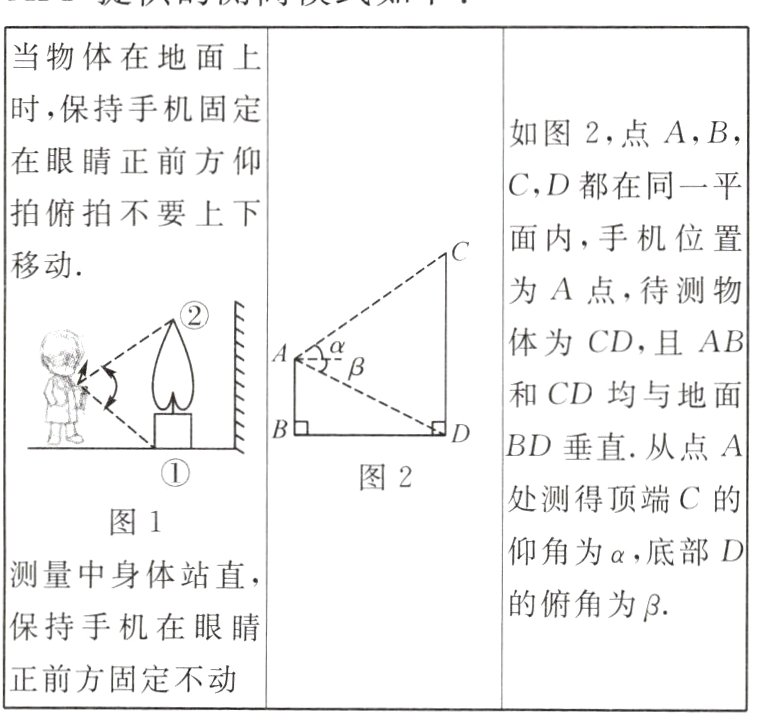
2.手机测距APP可以测量物体高度、宽度等,这些测距软件是基于几何学原理设计的.测量时只需要输入身高,再用手机拍摄功能将准星对准物体顶端和底部拍摄图片,程序就会计算出物体的高度,如图1某款测距APP提供的测高模式如下:
当物体在地面上时,保持手机固定在眼睛正前方仰拍俯拍不要上下移动.
如图2,点A,B,C,D都在同一平面内,手机位置为A点,待测物体为CD,且AB和CD均与地面BD垂直.从点A处测得顶端C的仰角为α,底部D的俯角为β.
某小组的同学想用上述方式手动计算某景区宣传广告牌的高度.如图2,经过测量得到AB=1.65 m,仰角α=35°,俯角β=28°,求出广告牌CD的高度.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,结果精确到0.1 m)
当物体在地面上时,保持手机固定在眼睛正前方仰拍俯拍不要上下移动.
如图2,点A,B,C,D都在同一平面内,手机位置为A点,待测物体为CD,且AB和CD均与地面BD垂直.从点A处测得顶端C的仰角为α,底部D的俯角为β.
某小组的同学想用上述方式手动计算某景区宣传广告牌的高度.如图2,经过测量得到AB=1.65 m,仰角α=35°,俯角β=28°,求出广告牌CD的高度.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,结果精确到0.1 m)

答案:
解:如图,过点A作$AG\perp CD$于点G.
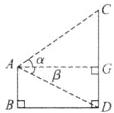
则$\angle CAG=\alpha = 35^{\circ},\angle DAG=\beta = 28^{\circ}$
$\because AB\perp BD,CD\perp BD$
$\therefore\angle ABD=\angle AGD=\angle BDG = 90^{\circ}$
$\therefore$四边形ABDG是矩形,$\therefore DG = AB = 1.65m$
在$Rt\triangle AGD$中,$\tan\beta=\frac{DG}{AG}$
$\therefore AG=\frac{DG}{\tan\beta}=\frac{1.65}{\tan28^{\circ}}$
在$Rt\triangle AGC$中,$\tan\alpha=\frac{CG}{AG}$
$\therefore CG = AG\cdot\tan\alpha=\frac{1.65}{\tan28^{\circ}}\cdot\tan35^{\circ}\approx\frac{1.65}{0.53}\times0.70\approx2.18(m)$
$\therefore CD = CG + DG\approx2.18 + 1.65\approx3.8(m)$
答:广告牌CD的高度约为3.8m.
解:如图,过点A作$AG\perp CD$于点G.

则$\angle CAG=\alpha = 35^{\circ},\angle DAG=\beta = 28^{\circ}$
$\because AB\perp BD,CD\perp BD$
$\therefore\angle ABD=\angle AGD=\angle BDG = 90^{\circ}$
$\therefore$四边形ABDG是矩形,$\therefore DG = AB = 1.65m$
在$Rt\triangle AGD$中,$\tan\beta=\frac{DG}{AG}$
$\therefore AG=\frac{DG}{\tan\beta}=\frac{1.65}{\tan28^{\circ}}$
在$Rt\triangle AGC$中,$\tan\alpha=\frac{CG}{AG}$
$\therefore CG = AG\cdot\tan\alpha=\frac{1.65}{\tan28^{\circ}}\cdot\tan35^{\circ}\approx\frac{1.65}{0.53}\times0.70\approx2.18(m)$
$\therefore CD = CG + DG\approx2.18 + 1.65\approx3.8(m)$
答:广告牌CD的高度约为3.8m.
查看更多完整答案,请扫码查看


