2025年畅行课堂九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年畅行课堂九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1.(2023·南充)如图,小兵同学从A处出发向正东方向走x米到达B处,再向正北方向走到C处,已知∠BAC=α,则A,C两处相距( )
A.$\frac{x}{\sin\alpha }$米
B.$\frac{x}{\cos\alpha }$米
C.$x\cdot\sin\alpha$米
D.$x\cdot\cos\alpha$米

A.$\frac{x}{\sin\alpha }$米
B.$\frac{x}{\cos\alpha }$米
C.$x\cdot\sin\alpha$米
D.$x\cdot\cos\alpha$米

答案:
B
2.如图,一艘轮船在M处观测到灯塔P位于南偏西30°方向,该轮船沿正南方向以15海里/时的速度匀速航行2小时后到达N处,再观测到灯塔P位于南偏西60°方向.若该轮船继续向南航行至离灯塔P最近的位置T处,则此时轮船与灯塔之间的距离PT为__________海里.(结果保留根号)


答案:
$15\sqrt{3}$
3.(2024·甘孜州)如图,一艘海轮位于灯塔P的北偏东37°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.这时,B处距离A处有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
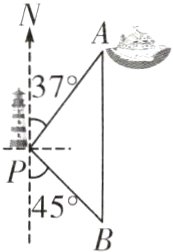

答案:
解:如图,过点P作PC⊥AB于点C,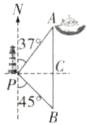
在Rt△ACP中,
∵∠A = 37°,AP = 100海里,
∴PC = AP·sinA = 100×sin37°≈100×0.60 = 60(海里),
AC = AP·cos37°≈100×0.80 = 80(海里).
在Rt△PCB中,
∵∠B = 45°,
∴BC = PC = 60(海里),
∴AB = AC + BC = 80 + 60 = 140(海里).
答:B处距离A处约有140海里.
解:如图,过点P作PC⊥AB于点C,

在Rt△ACP中,
∵∠A = 37°,AP = 100海里,
∴PC = AP·sinA = 100×sin37°≈100×0.60 = 60(海里),
AC = AP·cos37°≈100×0.80 = 80(海里).
在Rt△PCB中,
∵∠B = 45°,
∴BC = PC = 60(海里),
∴AB = AC + BC = 80 + 60 = 140(海里).
答:B处距离A处约有140海里.
4.如图,在滑轮的牵引下,一个滑块沿坡角为18°的斜坡向上移动了15 m,则此时滑块上升的高度是( )
A.15 m
B.15sin18° m
C.15cos18° m
D.15tan18° m
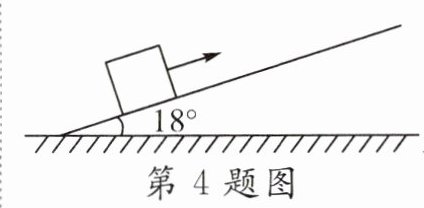
A.15 m
B.15sin18° m
C.15cos18° m
D.15tan18° m

答案:
B
5.(自贡中考)如图,我市在建高铁的某段路基横断面为梯形ABCD,DC//AB.BC长6米,坡角β为45°,AD的坡角α为30°,则AD长为______米(结果保留根号).


答案:
$6\sqrt{2}$
6.为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE=10 m,其坡度i1=1∶$\sqrt{3}$,将步梯DE改造为斜坡AF,其坡度i2=1∶4,求斜坡AF的长度.(结果精确到0.01 m,参考数据:$\sqrt{3}$≈1.732,$\sqrt{17}$≈4.123)
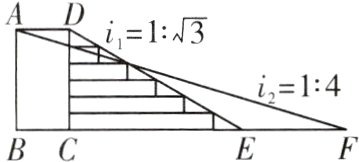

答案:
解:
∵DE = 10 m,其坡度$i_{1}=1:\sqrt{3}$,
∴在Rt△DCE中,$\tan\angle DEC=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$,
∴∠DEC = 30°,
∴$DC=\frac{1}{2}DE = 5$ m.
∵四边形ABCD为矩形,
∴AB = CD = 5 m.
∵斜坡AF的坡度$i_{2}=1:4$,
∴$\frac{AB}{BF}=\frac{1}{4}$,即BF = 4AB = 20 m.
在Rt△ABF中,由勾股定理,得$AF=\sqrt{AB^{2}+BF^{2}} = 5\sqrt{17}\approx20.62$(m).
答:斜坡AF的长度约为20.62 m.
∵DE = 10 m,其坡度$i_{1}=1:\sqrt{3}$,
∴在Rt△DCE中,$\tan\angle DEC=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$,
∴∠DEC = 30°,
∴$DC=\frac{1}{2}DE = 5$ m.
∵四边形ABCD为矩形,
∴AB = CD = 5 m.
∵斜坡AF的坡度$i_{2}=1:4$,
∴$\frac{AB}{BF}=\frac{1}{4}$,即BF = 4AB = 20 m.
在Rt△ABF中,由勾股定理,得$AF=\sqrt{AB^{2}+BF^{2}} = 5\sqrt{17}\approx20.62$(m).
答:斜坡AF的长度约为20.62 m.
7.(2024·泸州改编)如图,海中有一个小岛C,某渔船在海中的A点测得小岛C位于东北方向上,该渔船由西向东航行一段时间后到达B点,测得小岛C位于北偏西30°方向上,再沿北偏东60°方向继续航行一段时间后到达D点,这时测得小岛C位于北偏西60°方向上.已知A,C相距30 n mile.此时C,D间的距离为__________n mile(计算过程中的数据不取近似值).


答案:
$20\sqrt{2}$
查看更多完整答案,请扫码查看


