《2025年诚成教育学业评价七年级数学下册人教版》

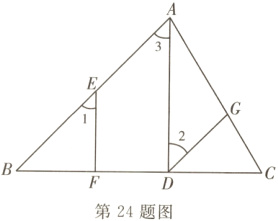
24. （8分）如图，已知AD⊥BC于点D，E为AB边上任意一点，EF⊥BC于点F，∠1 = ∠2.求证：∠BAC + ∠AGD = 180°.请把证明的过程填写完整.
证明：∵AD⊥BC，EF⊥BC（已知），
∴∠EFB = ∠ADB = 90°（______）.
∴EF//AD（______）.
∴∠1 = ∠3（______）.
又∠1 = ∠2（已知），
∴∠2 = ∠3（______）.
∴DG//AB（______）.
∴∠BAC + ∠AGD = 180°（______）.

答案： 解:垂直的定义.
　　　同位角相等，两直线平行.
　　　两直线平行，同位角相等.
　　　等量代换.
　　　内错角相等，两直线平行.
两直线平行，同旁内角互补.

25. （8分）阅读下面的文字，解答问题.
大家知道$\sqrt{2}$是无理数，而无理数是无限不循环小数，因此$\sqrt{2}$的小数部分我们不可能全部写出来，但是由于1 ＜ $\sqrt{2}$ ＜ 2，所以$\sqrt{2}$的整数部分为1，将$\sqrt{2}$减去其整数部分1，差就是小数部分，即为$\sqrt{2}$ - 1.解答下列问题：
（1）$\sqrt{10}$的整数部分是______，小数部分是______；
（2）如果$\sqrt{6}$的小数部分为a，$\sqrt{13}$的整数部分为b，求a + b - $\sqrt{6}$的值.

答案： 解:
(1)$3$，$\sqrt{10}-3$.
(2)$\because4\lt6\lt9$，$9\lt13\lt16$，
　　　　　$\therefore2\lt\sqrt{6}\lt3$，$3\lt\sqrt{13}\lt4$.
　　　　　$\therefore a=\sqrt{6}-2$，$b = 3$.
　　　　　$\therefore a + b-\sqrt{6}=\sqrt{6}-2 + 3-\sqrt{6}=1$.