《2025年诚成教育学业评价七年级数学下册人教版》

25. 新理念 阅读理解试题(10分)【阅读材料】
平面直角坐标系中，点P(x,y)的横坐标x的绝对值表示为|x|，纵坐标y的绝对值表示为|y|，我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫作点P(x,y)的勾股值，记为[P]，即[P]=|x|+|y|，如点P(1,2)的勾股值[P]=|1|+|2|=3.
【解决问题】
(1)求点A(-2,4)，B($\sqrt{2}+\sqrt{3}$,$\sqrt{2}-\sqrt{3}$)的勾股值[A]，[B]；
(2)若点M(x,y)在x轴的上方，其横、纵坐标均为整数，且[M]=3，求点M的坐标.

答案： 解:
(1)[A]=|-2|+|4|=2 + 4 = 6，
　　　　[B]=|$\sqrt{2}$ + $\sqrt{3}$|+|$\sqrt{2}$ - $\sqrt{3}$|
　　　　　　=$\sqrt{2}$ + $\sqrt{3}$ + $\sqrt{3}$ - $\sqrt{2}$
　　　　　　=2$\sqrt{3}$
(2)
∵点M(x,y)在x轴的上方，
　
　
∴y＞0.
　
　
∵点M的横、纵坐标均为整数，且[M]=|x|+|y|=3,
　
　
∴当y=1时,x=±2;
　　　　　当y=2时,x=±1;
　　　　　当y=3时,x=0.
　
　
∴点M的坐标为(−1,2)或(1,2)或(−2,1)或(2,1)或(0,3).

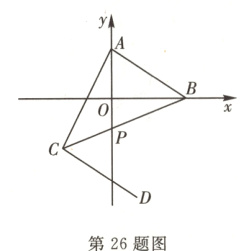
26. 新理念 综合探究试题(10分)如图，在平面直角坐标系中，点A，B在坐标轴上，其中A(0,a)，B(b,0)满足|2 - a|+$\sqrt{2b - 6}$=0.
(1)求A，B两点的坐标；
(2)将线段AB平移到CD，点A的对应点为C(-2,-2).
①写出点B的对应点D的坐标_______；
②连接AC，BC，BC交y轴于点P，已知三角形ABC的面积为8，求点P的坐标.

答案： 解:
(1)
∵|2−a|+$\sqrt{2b−6}$=0,
　　　　　|2−a|≥0,$\sqrt{2b−6}$≥0,
　
　
∴2−a=0,2b−6=0.
　　　　解得a=2,b=3.
　
　
∴A,B两点的坐标分别为(0,2)，(3,0).
(2)①(1,−4).
　　　　②设点P的坐标为(0,m)，
　　　　　则AP=2−m.
　
　
∵三角形ABC的面积=三角形APC的面积+三角形APB的面积，
　
　
∴$\frac{1}{2}$×2×(2−m)+$\frac{1}{2}$×3×(2−m)=8.
　　　　　解得m=−$\frac{6}{5}$.
　
　
∴点P的坐标为(0,−$\frac{6}{5}$).