《2025年诚成教育学业评价七年级数学下册人教版》

11.规定运算$a*b = |a - b|$，其中$a$，$b$为实数，则$(\sqrt{7}*3)+\sqrt{7}=$________.

答案： 3

12.$2a - 3$与$5 - a$是某个数的两个不同的平方根，则$a$的值为________.

答案： - 2

13.若$|2 - x|+\sqrt{y - 4}=0$，则$x^{y}$的算术平方根是________，$-xy$的立方根是________.

答案： 4 - 2

14.比较大小：$\frac{\sqrt{5}-1}{2}$________$\frac{3}{2}$(填“＞”“＜”或“=”).

答案： ＜

15.计算：$(-1)^{3}+|1 - \sqrt{2}|+\sqrt[3]{8}=$________.

答案： $\sqrt{2}$

16.若$-2x^{a}y$与$5x^{3}y^{b}$的和是单项式，则$(a + b)^{2}$的平方根是________.

答案： $\pm 4$

17.若$m＜\sqrt{28}＜m + 1$，且$m$为整数，则$m=$______←

答案： 5

18.如图，正方形$ABCD$的面积为3，点$A$在数轴上，且表示的数为-2，以点$A$为圆心，$AB$长为半径画弧，与数轴交于点$E$(点$E$在点$A$的右侧)，则点$E$所表示的数为________.

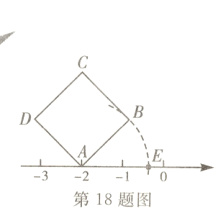
答案： $\sqrt{3}-2$

19.(8分)计算:
　(1)$(-3)^{2}+2\times(\sqrt{2}-1)-|-2\sqrt{2}|$；
　(2)$|1 - \sqrt{2}|+\sqrt[3]{-\frac{8}{27}}\times\sqrt{\frac{1}{4}}-\sqrt{2}$.

答案：
(1)7
(2)$-\frac{4}{3}$

20.(8分)解方程:
　(1)$(x - 2)^{3}=8$；　　　　　　　　　　　　(2)$64(x - 1)^{2}-1 = 0$.

答案：
(1)$x = 4$
(2)$x=\frac{9}{8}$或$x=\frac{7}{8}$

21.(5分)已知$a$，$b$互为相反数，$c$，$d$互为倒数，$m$的绝对值是4，求$2a+\sqrt{3cd}-m^{2}+2b$的值.

答案： 解：由题意，得$a + b = 0$，$cd = 1$，$|m| = 4$.
所以$2a+\sqrt{3cd}-m^{2}+2b$
$=2(a + b)+\sqrt{3cd}-m^{2}$
$=0+\sqrt{3}-4^{2}$
$=\sqrt{3}-16$.