《2025年诚成教育学业评价七年级数学下册人教版》

10.如图，正方形的周长为8个单位长度，在该正方形的4个顶点处分别标上0，2，4，6，先让正方形上表示数字6的点与数轴上表示 - 3的点重合，再将数轴按顺时针方向环绕在该正方形上，则正方形上与数轴上表示99的点重合的数字是( )
　　　　　　　　　　　　　　　　　　　　　　　　　　　　
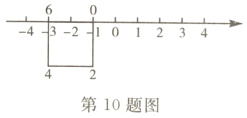
A.0
B.2
C.4
D.6

答案： C

11.已知$a,b$为两个连续整数，且$a \lt \sqrt{7} \lt b$，则$a + b =$_______.

答案： 5

12.若$3 + \sqrt{2}$与$3 - \sqrt{2}$的小数部分分别是$a,b$，则$\sqrt[3]{a + b} =$_______.

答案： 1

13.$x + 3$是4的平方根， - 8的立方根是$y - 1$，则$x + y =$_______.

答案： -2或 -6

14.在下列说法中：① - 4是16的平方根；②4的平方根是2；③$(-5)^{2}$的算术平方根是5；④$\sqrt{-2}$是一个负数；⑤0的相反数和倒数都是0；⑥$\sqrt{4} = \pm 2$.正确的是_______(填序号).

答案： ①③

15.新理念 新定义试题 规定$[m]$表示一个不大于实数$m$的最大整数，例如$[\frac{2}{3}]=0,[3.14]=3$.按此规定$[\sqrt{17} + 1]$的值为_______.

答案： 5

16.已知实数$a,b$满足$\sqrt{a - 1}+\sqrt{b + 2}=0$，则$(a + b)^{2022}$的立方根为_______.

答案： -1

17.若$|a|=\sqrt{6}$，则$-\sqrt{a^{2} - 2}$的相反数是_______.

答案： 2

18.实数$a,b,c$在数轴上的对应点的位置如图所示，化简$\sqrt{a^{2}}+|b - a|-\sqrt[3]{(a + b)^{3}}-|b - c|$的结果是_______.
　　
　　　　　　　　　　　　　　　　　　　　　　　　　

答案： -3a + b - c

19.(6分)计算:
(1)$5\sqrt{2}+3\sqrt{2}+|\sqrt{2}-2|+\sqrt[3]{8}$； (2)$\sqrt[3]{343}\times\sqrt{\frac{9}{49}}$.

答案：
(1)$7\sqrt{2}+4$ 
(2)3

20.(6分)求下列各式中$x$的值.
(1)$(x - 1)^{2}-9 = 0$； (2)$2(x - 3)^{3}+\frac{1}{4}=0$.

答案：
(1)x = 4或x = -2
(2)$x=\frac{5}{2}$