《2025年诚成教育学业评价七年级数学下册人教版》

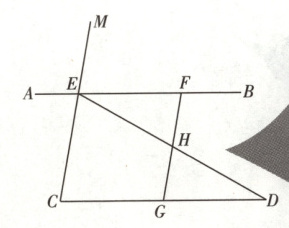
25.(10分) 如图,点E,F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C = ∠EFG,∠CED = ∠GHD.
(1)判断∠AED与∠D之间的数量关系,并说明理由;
(2)若∠EHF = 80°,∠D = 30°,求∠AEM的度数.

答案： 解：
(1)$∠AED + ∠D = 180°$.
理由如下：
∵$∠CED = ∠GHD$，
∴$CE// GF$.
∴$∠C = ∠FGD$.
∵$∠C = ∠EFG$，
∴$∠FGD = ∠EFG$.
∴$AB// CD$.
∴$∠AED + ∠D = 180°$.
(2)
∵$CE// GF$，
∴$∠CED = ∠EHF = 80°$.
∵$AB// CD$，
∴$∠BED = ∠D = 30°$.
∴$∠CEB = ∠CED + ∠BED = 110°$.
∴$∠AEM = ∠CEB = 110°$.

26.新理念 阅读理解试题 (12分) 阅读下面的文字,解答问题:
我们规定:用[x]表示实数x的整数部分,用＜ x ＞表示实数x的小数部分,例如:[3.14] = 3,＜ 3.14 ＞ = 0.14,[$\sqrt{2}$] = 1,＜ $\sqrt{2}$ ＞ = $\sqrt{2}$ - 1.因为$\sqrt{2}$的整数部分是1,将这个数减去其整数部分,差就是其小数部分.又例如:∵2² ＜ ($\sqrt{7}$)² ＜ 3²,∴2 ＜ $\sqrt{7}$ ＜ 3.∴[$\sqrt{7}$] = 2,＜ $\sqrt{7}$ ＞ = [$\sqrt{7}$] - 2.
请解答下列问题:
(1)[$\sqrt{14}$] = ______,＜ $\sqrt{14}$ ＞ = ______;
(2)如果＜ $\sqrt{5}$ ＞ = a,[$\sqrt{41}$] = b,求a + b - $\sqrt{5}$的平方根;
(3)求[$\sqrt{1}$] + [$\sqrt{2}$] + [$\sqrt{3}$] + [$\sqrt{4}$] + … + [$\sqrt{49}$]的值.

答案： 解：
(1)3，$\sqrt{14}-3$.
(2)
∵$2^{2}＜(\sqrt{5})^{2}＜3^{2}$，
∴$2＜\sqrt{5}＜3$.
∴$＜\sqrt{5}＞=\sqrt{5}-2$.
∴$a=\sqrt{5}-2$.
∵$6^{2}＜(\sqrt{41})^{2}＜7^{2}$，
∴$6＜\sqrt{41}＜7$.
∴$b=[\sqrt{41}]=6$.
∴$a + b-\sqrt{5}=\sqrt{5}-2 + 6-\sqrt{5}=4$.
∴$a + b-\sqrt{5}$的平方根为±2.
(3)
∵$2^{2}-1^{2}=3$，$3^{2}-2^{2}=5$，
$4^{2}-3^{2}=7$，$5^{2}-4^{2}=9$，
$6^{2}-5^{2}=11$，$7^{2}-6^{2}=13$，
∴$[\sqrt{1}]+[\sqrt{2}]+[\sqrt{3}]+[\sqrt{4}]+\cdots+[\sqrt{49}]$
$=1×3 + 2×5 + 3×7 + 4×9$
$+5×11 + 6×13 + 7$
$=210$.