《2025年诚成教育学业评价七年级数学下册人教版》

10. 如图，小颖利用直尺和含30°角的三角尺，依次画出了直线a，b，c，若∠1=70°，则∠2的度数为 ( )

A. 110°
B. 70°
C. 40°
D. 30°

答案： C

11. “两个锐角的和是钝角”是______命题(填“真”或“假”).

答案： 假

12. 如图，“若a//b，b//c，则a//c”的依据是____________________.

答案： 平行于同一条直线的两条直线平行

13. 若x，y为实数，且满足$\sqrt{x - 2}+|y + 5|=0$，则xy=______.

答案： - 10

14. 如图，把一张长方形纸片ABCD沿EF折叠后，点D，C分别落在点M，N的位置上，EM与BC的交点为G，若∠EFG=65°，则∠1的度数为______.

答案： 130°

15. 如果一个角的两边分别平行于另一个角的两边，那么这两个角的关系是______.

答案： 相等或互补

16. 8条直线相交于一点，有______对邻补角.

答案： 112

17. 若数a和2a－9都是一个正数m的平方根，则a的值为______.

答案： 3或9

18. 将一副直角三角板按如图所示的方式叠放在一起，其中点B，D重合，若固定三角板AOB，将三角板ACD绕着公共顶点A，按逆时针方向旋转α度(90＜α＜180)，当旋转后的CD与三角板AOB的某一边平行时，α的值为______.

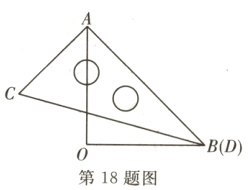
答案： 150或105

19. (8分) 把下列各数填在相应的表示集合的大括号内.
－6，π，－$\frac{2}{3}$，－|－3|，$\frac{22}{7}$，－0.4，1.6，$\sqrt{6}$，0，1.101 001 000 1…(每两个1之间依次多一个0).
整数：{ ，…}；负分数：{ ，…}；
无理数：{ ，…}.

答案： -6，-|-3|，0，
$-\frac{2}{3}$，-0.4，
$\pi$，$\sqrt{6}$，1.101 001 000 1…(每两个1之间依次多一个0)

20. (12分) 计算：
(1) $\sqrt{81}-\sqrt{\frac{1}{25}}+\sqrt{0.49}$； (2) $(\sqrt{3})^2-\sqrt{(-6)^2}\times\frac{1}{\sqrt{36}}$；
(3) $\sqrt[3]{-27}-(\sqrt[3]{8}+4)\div\sqrt{3^2}$； (4) |1 - $\sqrt{2}$|+|$\sqrt{2}-\sqrt{3}$|+|$\sqrt{2}-1$|.

答案：
(1)9.5　
(2)2　
(3)-5　
(4)$\sqrt{2}-2+\sqrt{3}$