2025年新编高中同步作业高中数学选择性必修第二册人教版A
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新编高中同步作业高中数学选择性必修第二册人教版A 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
问题式预习
知识点 函数的单调性与导数
定义在区间$(a,b)$内的函数$y = f(x)$:
|$f^{\prime}(x)$的正负|$f(x)$的单调性|
|----|----|
|$f^{\prime}(x)>0$|单调递____|
|$f^{\prime}(x)0$|单调递____|
[微训练]
知识点 函数的单调性与导数
定义在区间$(a,b)$内的函数$y = f(x)$:
|$f^{\prime}(x)$的正负|$f(x)$的单调性|
|----|----|
|$f^{\prime}(x)>0$|单调递____|
|$f^{\prime}(x)0$|单调递____|
[微训练]
答案:
增@@减
1. 判断(正确的打“√”,错误的打“×”).
(1)对于函数$y = f(x)$,在区间$I$上,若$f^{\prime}(x)0$,则$f(x)$在$I$上单调递减. ( )
(2)对于函数$y = f(x)$,在区间$I$上,若$f(x)$是单调递增的,则$f^{\prime}(x)>0$. ( )
(1)对于函数$y = f(x)$,在区间$I$上,若$f^{\prime}(x)0$,则$f(x)$在$I$上单调递减. ( )
(2)对于函数$y = f(x)$,在区间$I$上,若$f(x)$是单调递增的,则$f^{\prime}(x)>0$. ( )
答案:
√@@× 提示:$f^{\prime}(x)=0$也有可能,如$y = x^{3}$。
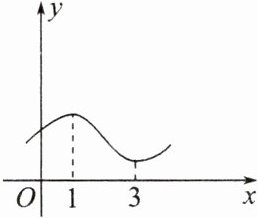
2. 函数$y = f(x)$的图象如图所示,则在区间$(1,3)$内,有( )
A. $f^{\prime}(x)>0$
B. $f^{\prime}(x)0$
C. $f^{\prime}(x)=0$
D. $f^{\prime}(x)$的符号不确定

A. $f^{\prime}(x)>0$
B. $f^{\prime}(x)0$
C. $f^{\prime}(x)=0$
D. $f^{\prime}(x)$的符号不确定
答案:
B 解析:在区间$(1,3)$内,函数$y = f(x)$的图象是下降的,函数单调递减,所以$f^{\prime}(x)0$。
任务型课堂
任务一 由图象理解导数的正负与函数的单调性
[探究活动]
已知下列 $A$,$B$ 两组函数:
$A$:(1)$y = 2x - 1$,(2)$y = 2^{x}$,(3)$y = x^{3}$;
$B$:(1)$y = - 3x$,(2)$y = (\frac{1}{3})^{x}$,(3)$y = \frac{1}{x}$ ($x>0$).
探究 1:$A$,$B$ 两组函数分别是增函数还是减函数?
探究 2:计算两组函数的导数,你能判断导数的正负吗?
探究 3:结合探究 1、探究 2 的结论,你有何猜想?
[评价活动]
任务一 由图象理解导数的正负与函数的单调性
[探究活动]
已知下列 $A$,$B$ 两组函数:
$A$:(1)$y = 2x - 1$,(2)$y = 2^{x}$,(3)$y = x^{3}$;
$B$:(1)$y = - 3x$,(2)$y = (\frac{1}{3})^{x}$,(3)$y = \frac{1}{x}$ ($x>0$).
探究 1:$A$,$B$ 两组函数分别是增函数还是减函数?
探究 2:计算两组函数的导数,你能判断导数的正负吗?
探究 3:结合探究 1、探究 2 的结论,你有何猜想?
[评价活动]
答案:
A组中的函数都是增函数,B组中的函数都是减函数。@@A组:
(1)$y' = 2>0$,
(2)$y' = 2^x\ln 2>0$,
(3)$y' = 3x^2\geq0$。 B组:
(1)$y' = -30$,
(2)$y' = (\frac{1}{3})^x\ln\frac{1}{3}0$,
(3)$y' = -\frac{1}{x^2}0$。@@导数的正负决定函数的单调性。
(1)$y' = 2>0$,
(2)$y' = 2^x\ln 2>0$,
(3)$y' = 3x^2\geq0$。 B组:
(1)$y' = -30$,
(2)$y' = (\frac{1}{3})^x\ln\frac{1}{3}0$,
(3)$y' = -\frac{1}{x^2}0$。@@导数的正负决定函数的单调性。
查看更多完整答案,请扫码查看


