2025年新编高中同步作业高中数学选择性必修第二册人教版A
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新编高中同步作业高中数学选择性必修第二册人教版A 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 已知数列的通项公式是$a_{n}=\begin{cases}3n + 1,n是奇数,\\2n - 2,n是偶数,\end{cases}$则$a_{4}=$________,$a_{5}=$________.
答案:
6@@16
2. 写出下列数列$\{a_{n}\}$的一个通项公式:
(1)$3,5,9,17,33,\cdots$;
(2)$11,102,1003,10004,\cdots$;
(3)$1\frac{1}{2},2\frac{4}{5},3\frac{9}{10},4\frac{16}{17},\cdots$;
(4)$2,-6,12,-20,30,-42,\cdots$.
(1)$3,5,9,17,33,\cdots$;
(2)$11,102,1003,10004,\cdots$;
(3)$1\frac{1}{2},2\frac{4}{5},3\frac{9}{10},4\frac{16}{17},\cdots$;
(4)$2,-6,12,-20,30,-42,\cdots$.
答案:
解:因为$a_{1}=3 = 2^{1}+1$,$a_{2}=5 = 2^{2}+1$,$a_{3}=9 = 2^{3}+1$,$a_{4}=17 = 2^{4}+1$,$a_{5}=33 = 2^{5}+1$,…,所以该数列的一个通项公式为$a_{n}=2^{n}+1$。@@这个数列可以改写为 10 + 1,100 + 2,1000 + 3,10000 + 4,…,所以该数列的一个通项公式是$a_{n}=10^{n}+n$。@@因为$1\frac{1}{2}=1+\frac{1^{2}}{1^{2}+1}$,$2\frac{4}{5}=2+\frac{2^{2}}{2^{2}+1}$,$3\frac{9}{10}=3+\frac{3^{2}}{3^{2}+1}$,$4\frac{16}{17}=4+\frac{4^{2}}{4^{2}+1}$,…,所以该数列的一个通项公式为$a_{n}=n+\frac{n^{2}}{n^{2}+1}$。@@将数列变形为 1×2, - 2×3,3×4, - 4×5,5×6, - 6×7,…,所以该数列的一个通项公式为$a_{n}=(-1)^{n + 1}\cdot n(n + 1)$。
任务三 数列的函数特性
[探究活动]
某地某段时间流感每日确诊病例变化曲线如图所示. 设该地这段时间的流感每日确诊人数按日期先后顺序构成数列$\{a_{n}\}$.
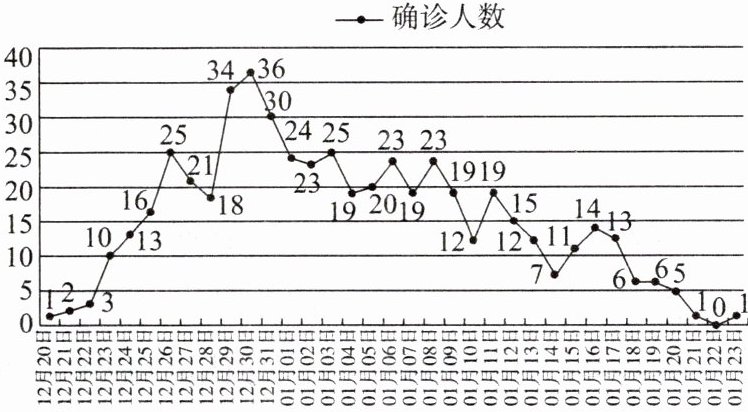
探究1:数列$\{a_{n}\}$是递增数列吗? 是递减数列吗?
探究2:数列$\{a_{n}\}$的前$7$项是递增数列吗? 数列$\{a_{n}\}$的后$5$项是递减数列吗?
探究3:数列$\{a_{n}\}$的最大项与最小项分别为第几项?
[探究活动]
某地某段时间流感每日确诊病例变化曲线如图所示. 设该地这段时间的流感每日确诊人数按日期先后顺序构成数列$\{a_{n}\}$.

探究1:数列$\{a_{n}\}$是递增数列吗? 是递减数列吗?
探究2:数列$\{a_{n}\}$的前$7$项是递增数列吗? 数列$\{a_{n}\}$的后$5$项是递减数列吗?
探究3:数列$\{a_{n}\}$的最大项与最小项分别为第几项?
答案:
都不是。@@前 7 项是递增数列,后 5 项不是递减数列。@@最大项是$a_{11}=36$,最小项是$a_{34}=0$。
查看更多完整答案,请扫码查看


