2025年新编高中同步作业高中数学选择性必修第二册人教版A
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新编高中同步作业高中数学选择性必修第二册人教版A 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 已知数列$\{ a_{n}\}$的通项公式为$a_{n}=n^{2}-7n - 8$.
(1)数列中为负数的项的个数是________;
(2)该数列的最小项为________.
(1)数列中为负数的项的个数是________;
(2)该数列的最小项为________.
答案:
7@@-20
2. 已知数列$\{ a_{n}\}$的通项公式为$a_{n}=3n^{2}-28n$.
(1)这个数列的第 4 项是________,第 6 项是________;
(2)$-49$是该数列的第________项;
(3)68 是该数列的项吗?
(1)这个数列的第 4 项是________,第 6 项是________;
(2)$-49$是该数列的第________项;
(3)68 是该数列的项吗?
答案:
(1)根据\(a_{n}=3n^{2}-28n\), 得\(a_{4}=3\times4^{2}-28\times4=-64\), \(a_{6}=3\times6^{2}-28\times6=-60\)。
(2)令\(3n^{2}-28n=-49\), 即\(3n^{2}-28n + 49 = 0\),解得\(n = 7\)或\(n=\frac{7}{3}\)(舍)。 所以\(-49\)是该数列的第7项。
(3)令\(3n^{2}-28n = 68\),即\(3n^{2}-28n - 68 = 0\), 解得\(n=-2\)或\(n=\frac{34}{3}\),均不是正整数。 所以68不是数列\(\{a_{n}\}\)中的项。
(1)根据\(a_{n}=3n^{2}-28n\), 得\(a_{4}=3\times4^{2}-28\times4=-64\), \(a_{6}=3\times6^{2}-28\times6=-60\)。
(2)令\(3n^{2}-28n=-49\), 即\(3n^{2}-28n + 49 = 0\),解得\(n = 7\)或\(n=\frac{7}{3}\)(舍)。 所以\(-49\)是该数列的第7项。
(3)令\(3n^{2}-28n = 68\),即\(3n^{2}-28n - 68 = 0\), 解得\(n=-2\)或\(n=\frac{34}{3}\),均不是正整数。 所以68不是数列\(\{a_{n}\}\)中的项。
任务二 数列的递推公式
[探究活动]
在“贪吃蛇”的游戏中,设定贪吃蛇从原点出发,沿着如图所示的逆时针方向螺旋式前进,不停地吞食沿途的每一个格点(不包括原点). 已知贪吃蛇的初始长度为 0,并且每吞食一个格点,长度就增加 1 个单位,如它的头部到达点$P_{1}(1,1)$,其长度增加到 2,它的头部到达点$P_{2}(2,2)$,其长度增加到 12.
[评价活动]
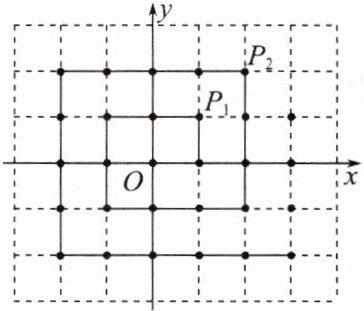
探究 1:当贪吃蛇的头部到达点$P_{3}(3,3)$时,它的长度增加到多少?
探究 2:当贪吃蛇的头部到达点$P_{9}(9,9)$时,它的长度增加到多少?
[探究活动]
在“贪吃蛇”的游戏中,设定贪吃蛇从原点出发,沿着如图所示的逆时针方向螺旋式前进,不停地吞食沿途的每一个格点(不包括原点). 已知贪吃蛇的初始长度为 0,并且每吞食一个格点,长度就增加 1 个单位,如它的头部到达点$P_{1}(1,1)$,其长度增加到 2,它的头部到达点$P_{2}(2,2)$,其长度增加到 12.
[评价活动]

探究 1:当贪吃蛇的头部到达点$P_{3}(3,3)$时,它的长度增加到多少?
探究 2:当贪吃蛇的头部到达点$P_{9}(9,9)$时,它的长度增加到多少?
答案:
任务二 【探究活动】 探究1:设贪吃蛇的头部到达点\(P_{n}(n,n)\)时的长度为\(a_{n}\),则\(a_{1}=2,a_{2}=a_{1}+10 = 12,a_{3}=a_{2}+18 = 30\)。 探究2:由探究1,\(a_{1}=2\), \(a_{2}=a_{1}+10\),即\(a_{2}-a_{1}=10\), \(a_{3}=a_{2}+18\),即\(a_{3}-a_{2}=18\), …… 以此类推:\(a_{n}-a_{n - 1}=8n - 6(n\geqslant2)\), 则有\(a_{n}=(a_{n}-a_{n - 1})+(a_{n - 1}-a_{n - 2})+\cdots+(a_{2}-a_{1})+a_{1}=4n^{2}-2n\), 当\(n = 9\)时,有\(a_{9}=306\)。
查看更多完整答案,请扫码查看


