2025年新编高中同步作业高中数学选择性必修第二册人教版A
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新编高中同步作业高中数学选择性必修第二册人教版A 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1.(多选)已知数列$\{ a_{n}\}$的通项公式为$a_{n}=2n + 5$,则此数列 ( )
A. 是公差为$2$的递增等差数列
B. 是公差为$2$的递减等差数列
C. 是首项为$7$的递减等差数列
D. 是首项为$7$的递增等差数列
A. 是公差为$2$的递增等差数列
B. 是公差为$2$的递减等差数列
C. 是首项为$7$的递减等差数列
D. 是首项为$7$的递增等差数列
答案:
AD
2. 在等差数列$\{ a_{n}\}$中,首项$a_{1}=5$,公差$d = 3$,则当$a_{n}=2024$时,$n$等于 ( )
A. $671$
B. $672$
C. $673$
D. $674$
A. $671$
B. $672$
C. $673$
D. $674$
答案:
D
1.(多选)下列说法正确的是 ( )
A. 若$a - b = b - c$,则$a$,$b$,$c$成等差数列
B. 若$a_{n}-a_{n - 1}=n(n\in\mathbf{N}^{*}$且$n > 1)$,则$\{ a_{n}\}$是等差数列
C. 等差数列是相邻两项中的后项与前项之差都等于同一个常数的数列
D. 等差数列的公差是该数列中任意两项的差
A. 若$a - b = b - c$,则$a$,$b$,$c$成等差数列
B. 若$a_{n}-a_{n - 1}=n(n\in\mathbf{N}^{*}$且$n > 1)$,则$\{ a_{n}\}$是等差数列
C. 等差数列是相邻两项中的后项与前项之差都等于同一个常数的数列
D. 等差数列的公差是该数列中任意两项的差
答案:
AC@@解析:对于A,由a - b = b - c,可得a + c = 2b,因此a,b,c成等差数列,A正确;对于B,n不是固定常数,该数列不是等差数列,B错误;对于C,根据等差数列的定义可知,C正确;对于D,应为相邻两项。
2. 若数列$\{ a_{n}\}$是等差数列,且$a_{n}=an^{2}+n$,则实数$a =$________.
答案:
0@@解析:因为{an}是等差数列,所以an + 1 - an为常数,所以[a(n + 1)² + (n + 1)] - (an² + n) = 2an + a + 1为常数,所以2a = 0,所以a = 0。
3. 若$m$和$2n$的等差中项为$4$,$2m$和$n$的等差中项为$5$,则$m$与$n$的等差中项是________.
答案:
3@@解析:由m和2n的等差中项为4,得m + 2n = 8。
由2m和n的等差中项为5,得2m + n = 10。
两式相加,得m + n = 6。所以m与n的等差中项为(m + n)/2 = 6/2 = 3。
任务二 等差数列的通项公式
[探究活动]
我国古代天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度). 二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始. 每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),以冬至的晷长为首项,夏至的晷长为最后一项,按图中顺时针方向,由每个节气的晷长构成的数列为$\{ a_{n}\}$.
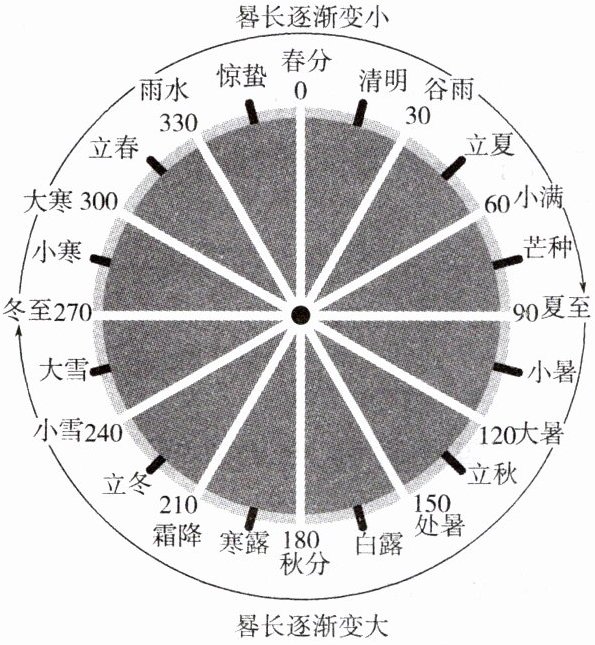
探究 1:数列$\{ a_{n}\}$是等差数列吗?
探究 2:相邻两个节气晷长减少的量是多少?
探究 3:春分的晷长为多少?
[探究活动]
我国古代天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度). 二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始. 每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),以冬至的晷长为首项,夏至的晷长为最后一项,按图中顺时针方向,由每个节气的晷长构成的数列为$\{ a_{n}\}$.

探究 1:数列$\{ a_{n}\}$是等差数列吗?
探究 2:相邻两个节气晷长减少的量是多少?
探究 3:春分的晷长为多少?
答案:
因为相邻两个节气晷长减少的量相同,所以数列{an}是等差数列。
@@由题意知,等差数列{an},公差为d,则a1 = 135,a13 = 15,解得d = - 10。 所以相邻两个节气晷长减少的量为一尺。
@@因为a1 = 135,d = - 10,所以an = - 10n + 145,a7 = - 10×7 + 145 = 75。所以春分的晷长为七尺五寸。
@@由题意知,等差数列{an},公差为d,则a1 = 135,a13 = 15,解得d = - 10。 所以相邻两个节气晷长减少的量为一尺。
@@因为a1 = 135,d = - 10,所以an = - 10n + 145,a7 = - 10×7 + 145 = 75。所以春分的晷长为七尺五寸。
查看更多完整答案,请扫码查看


