《2025年初中必刷题七年级数学下册苏科版》

1[2024湖南郴州期末,中]已知关于x的不等式2x≥a - 1的解集是x≥ - 1,则a的值是________.

答案： -1 【解析】因为2x≥a - 1，所以x≥$\frac{a - 1}{2}$。因为不等式2x≥a - 1的解集是x≥ - 1，所以$\frac{a - 1}{2}$= - 1，所以a = - 1。故答案为 - 1。

2[2024山东聊城期末,中]若关于x的不等式组$\begin{cases}-x + 2 ＜ x - 8 \\x ＞ m\end{cases}$的解集为x ＞ 5,则m的取值范围为________.

答案： m≤5 【解析】$\begin{cases}-x + 2 ＜ x - 8,① \\ x ＞ m,②\end{cases}$由不等式①，得x＞5，由不等式②，得x＞m。因为不等式组$\begin{cases}-x + 2 ＜ x - 8 \\ x ＞ m\end{cases}$的解集为x＞5，所以m≤5，故答案为m≤5。

3[2024河北唐山期末,中]关于x的不等式组$\begin{cases}x - a ＞ - 1 \\x - a ≤ 2\end{cases}$的解集中,任意一个x的值均在3≤x ＜ 7的范围内,则a的取值范围为________.

答案： 4≤a＜5 【解析】由$\begin{cases}x - a ＞ - 1 \\ x - a ≤ 2\end{cases}$得$\begin{cases}x ＞ a - 1 \\ x ≤ a + 2\end{cases}$。因为不等式的解集中，任意一个x的值均在3≤x＜7的范围内，所以有$\begin{cases}a - 1 ≥ 3 \\ a + 2 ＜ 7\end{cases}$，解得4≤a＜5。故答案为4≤a＜5。

4[2024河北邢台期末,中]关于x的一元一次不等式组$\begin{cases}x + 1 ≥ 3 \\4x - 16 ＜ - 2a\end{cases}$有解,则a的取值范围是（ ）
A. a≥4
B. a ＞ 4
C. a≤4
D. a ＜ 4

答案： D 【解析】$\begin{cases}x + 1 ≥ 3,① \\ 4x - 16 ＜ - 2a,②\end{cases}$解不等式①得x≥2，解不等式②得x＜4 - $\frac{1}{2}$a。因为关于x的一元一次不等式组$\begin{cases}x + 1 ≥ 3 \\ 4x - 16 ＜ - 2a\end{cases}$有解，所以4 - $\frac{1}{2}$a＞2，解得a＜4。故选D。

5[2024河北张家口万全区期末,中]若关于x的不等式组$\begin{cases}x - a ＞ 3 \\1 - 2x ＞ x - 2\end{cases}$无解,则a的取值范围是（ ）
A. a ＜ - 2
B. a≤ - 2
C. a ＞ - 2
D. a≥ - 2

答案： D 【解析】由x - a＞3，得x＞a + 3，由1 - 2x＞x - 2，得x＜1。因为不等式组无解，所以a + 3≥1，解得a≥ - 2，故选D。

6[2024河北张家口期末,中]若关于x的不等式组$\begin{cases}3 - (x - 1) ≥ 2 \\5x - a ＞ 4x\end{cases}$有且只有3个整数解,则a的取值范围在数轴上表示为（ ）

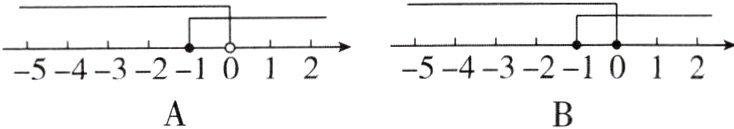
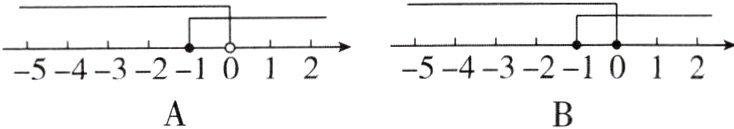
答案： A 【解析】$\begin{cases}3 - (x - 1) ≥ 2,① \\ 5x - a ＞ 4x,②\end{cases}$解不等式①，得x≤2，解不等式②，得x＞a。因为该不等式组有解，所以不等式组的解集是a＜x≤2。因为关于x的不等式组$\begin{cases}3 - (x - 1) ≥ 2 \\ 5x - a ＞ 4x\end{cases}$有且只有3个整数解，所以这三个整数解是0，1，2，所以 - 1≤a＜0，故选A。

7[2024重庆江津区期末,中]若关于x的一元一次不等式组$\begin{cases}\frac{x + 3}{2} ≤ 4 \\2x - a ≥ 2\end{cases}$至少有2个整数解,则a的取值范围是________.

答案： a≤6 【解析】解不等式组得$\frac{a + 2}{2}$≤x≤5。由题意得$\frac{a + 2}{2}$≤4，解得a≤6。

8[2024河北廊坊期末，中]已知不等式组$\begin{cases}1 - 2(x - 1) ≤ 5 \\\frac{3x - a}{2} ＜ x + \frac{1}{2}\end{cases}$的整数解是 - 1,0,1,2,确定字母a的取值范围.

答案： 【解】$\begin{cases}1 - 2(x - 1) ≤ 5,① \\ \frac{3x - a}{2} ＜ x + \frac{1}{2},②\end{cases}$
解不等式①得x≥ - 1，
解不等式②得x＜a + 1。
因为不等式组有解，
所以不等式组的解集是 - 1≤x＜a + 1。
因为不等式组的整数解是 - 1，0，1，2，
所以2＜a + 1≤3，解得1＜a≤2。

9[2024河南周口质检,中]若关于x,y的二元一次方程组$\begin{cases}3x + y = 1 + a \\x + 3y = 3\end{cases}$的解中,x是非负数,y的值不大于 - 1,则a的取值范围为________.

答案： a≥16 【解析】解关于x，y的二元一次方程组$\begin{cases}3x + y = 1 + a \\ x + 3y = 3\end{cases}$得$\begin{cases}x = \frac{3}{8}a \\ y = \frac{8 - a}{8}\end{cases}$。因为x是非负数，y的值不大于 - 1，所以$\begin{cases}\frac{3}{8}a ≥ 0 \\ \frac{8 - a}{8} ≤ - 1\end{cases}$，解得a≥16。

10[2024山东威海期末,中]已知关于x,y的方程组$\begin{cases}3x + 4y = m - 5 \\4x + 3y = 3m + 1\end{cases}$的解满足x + y ＜ 0,x - y ＞ 0,则m的取值范围为________.

答案： - 3＜m＜1 【解析】$\begin{cases}3x + 4y = m - 5,① \\ 4x + 3y = 3m + 1,②\end{cases}$① + ②得7x + 7y = 4m - 4，则x + y = $\frac{4m - 4}{7}$，② - ①得x - y = 2m + 6。因为x + y＜0，x - y＞0，所以$\begin{cases}\frac{4m - 4}{7} ＜ 0 \\ 2m + 6 ＞ 0\end{cases}$，所以 - 3＜m＜1，故答案为 - 3＜m＜1。