第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1[中]若$ax^{2}+2x+\frac{a}{8}=(2x+\frac{1}{2})^{2}+m$,则$a,m$的值分别是( )
A. 2,0
B. 2,$\frac{1}{4}$
C. 4,$\frac{1}{4}$
D. $\frac{1}{4}$,4
A. 2,0
B. 2,$\frac{1}{4}$
C. 4,$\frac{1}{4}$
D. $\frac{1}{4}$,4
答案:
C 【解析】由$ax^{2}+2x+\frac{a}{8}=(2x+\frac{1}{2})^{2}+m = 4x^{2}+2x+\frac{1}{4}+m$,得$a = 4$,且$\frac{a}{8}=\frac{1}{4}+m$,则$m=\frac{1}{4}$。
2[2024江苏常州期中,中]已知$(2024 - x)(x - 2023)= - 2$,则$(2024 - x)^{2}+(x - 2023)^{2}$的值是( )
A. 7
B. 6
C. 5
D. 4
A. 7
B. 6
C. 5
D. 4
答案:
C 【解析】因为$(2024 - x)(x - 2023)= - 2$,$2024 - x + x - 2023 = 1$,所以$(2024 - x)^{2}+(x - 2023)^{2}=[(2024 - x)+(x - 2023)]^{2}-2(2024 - x)(x - 2023)=1 - 2\times(-2)=1 + 4 = 5$。故选 C。
3[2024江苏镇江期中,较难]如图,若一个长方形广场的长为18米,宽为10米,现因施工改造,将广场的长和宽各增加$x$米,广场面积增加了20平方米,同时沿长方形广场的四边分别向外修建半圆形花圃.请你计算出花圃的总面积为( )
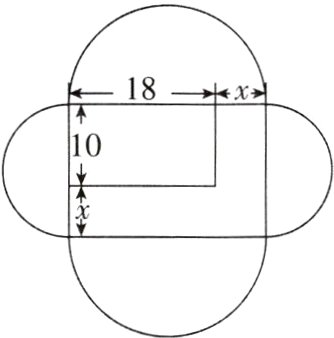
A. 90π平方米
B. 116π平方米
C. 120π平方米
D. 128π平方米

A. 90π平方米
B. 116π平方米
C. 120π平方米
D. 128π平方米
答案:
B 【解析】设扩大后的长方形广场的长为$a=(18 + x)$米,宽为$b=(10 + x)$米。依题意,得$ab = 18\times10 + 20 = 200$,$a - b=(18 + x)-(10 + x)=8$,所以$a^{2}+b^{2}=(a - b)^{2}+2ab = 8^{2}+2\times200 = 464$,所以花圃的总面积为$(\frac{a}{2})^{2}\pi+(\frac{b}{2})^{2}\pi=\frac{(a^{2}+b^{2})}{4}\pi=\frac{464}{4}\pi = 116\pi$(平方米)。故选 B。
4[中]已知$x = - 2,y = \frac{1}{2}$,则$(x + 2y)^{2}-(x + y)(x - y)$的值为_______.
答案:
$-\frac{11}{4}$【解析】原式$=x^{2}+4xy + 4y^{2}-(x^{2}-y^{2})=x^{2}+4xy + 4y^{2}-x^{2}+y^{2}=5y^{2}+4xy$。当$x = - 2$,$y=\frac{1}{2}$时,原式$=5\times\frac{1}{4}-4=-\frac{11}{4}$。
5[中]若$(2a + b)^{2}=17,(a - 2b)^{2}=8$,则$3a^{2}+3b^{2}$的值为_______.
答案:
15 【解析】由$(2a + b)^{2}=4a^{2}+4ab + b^{2}$,$(a - 2b)^{2}=a^{2}-4ab + 4b^{2}$,得$(2a + b)^{2}+(a - 2b)^{2}=5a^{2}+5b^{2}=25$,则$a^{2}+b^{2}=5$,所以$3(a^{2}+b^{2})=3a^{2}+3b^{2}=15$。
6[2023江苏镇江期中,中]若关于$x$的多项式$4x^{2}+(m - 1)x + 9$是完全平方式,则$m$的值为_______.
答案:
13 或 - 11 【解析】因为关于$x$的多项式$4x^{2}+(m - 1)x + 9$是完全平方式,所以$(m - 1)x=\pm2\times3\times2x$。当$(m - 1)x = 2\times3\times2x = 12x$时,$m = 13$;当$(m - 1)x=-2\times3\times2x=-12x$时,$m = - 11$。综上所述,$m$的值为 13 或 - 11。
7[2024四川成都质检,中]计算:$\frac{2013×2014 - 1}{2013 + 2012×2014}$.
答案:
【解】$\frac{2013\times2014 - 1}{2013 + 2012\times2014}$
$=\frac{2013\times(2013 + 1)-1}{2013+(2013 - 1)(2013 + 1)}$
$=\frac{2013^{2}+2013 - 1}{2013 + 2013^{2}-1}$
$=\frac{2013^{2}+2012}{2013^{2}+2012}=1$。
$=\frac{2013\times(2013 + 1)-1}{2013+(2013 - 1)(2013 + 1)}$
$=\frac{2013^{2}+2013 - 1}{2013 + 2013^{2}-1}$
$=\frac{2013^{2}+2012}{2013^{2}+2012}=1$。
8[2024江苏南京期末,中]先化简,再求值:$(2x - y)^{2}-(x - y)(x + y)-2y^{2}$,其中$x = 2,y = - 3$.
答案:
【解】$(2x - y)^{2}-(x - y)(x + y)-2y^{2}=4x^{2}-4xy + y^{2}-x^{2}+y^{2}-2y^{2}=3x^{2}-4xy$。
当$x = 2$,$y = - 3$时,原式$=3\times2^{2}-4\times2\times(-3)=36$。
当$x = 2$,$y = - 3$时,原式$=3\times2^{2}-4\times2\times(-3)=36$。
9核心素养模型思想[较难]对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如,由图(1)可以得到$(a + b)^{2}=a^{2}+2ab + b^{2}$,请解答下列问题:
(1)写出图(2)所表示的数学等式.

 图(2)
图(2)
(2)利用(1)中得到的结论,解决下面的问题:若$a + b + c = 10,ab + ac + bc = 35$,则$a^{2}+b^{2}+c^{2}=$________.
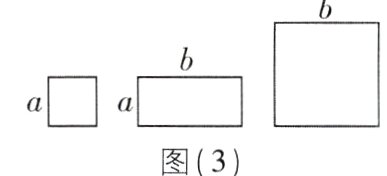
(3)小明同学用图(3)中$x$张边长为$a$的正方形纸片、$y$张边长为$b$的正方形纸片和$z$张边长分别为$a,b$的长方形纸片拼出一个面积为$(5a + 7b)(9a + 4b)$的长方形,则$x + y + z=$_______.
(1)写出图(2)所表示的数学等式.

 图(2)
图(2)(2)利用(1)中得到的结论,解决下面的问题:若$a + b + c = 10,ab + ac + bc = 35$,则$a^{2}+b^{2}+c^{2}=$________.
(3)小明同学用图(3)中$x$张边长为$a$的正方形纸片、$y$张边长为$b$的正方形纸片和$z$张边长分别为$a,b$的长方形纸片拼出一个面积为$(5a + 7b)(9a + 4b)$的长方形,则$x + y + z=$_______.

答案:
【解】
(1) 题图
(2)中图形的面积既可以表示为$(a + b + c)^{2}$,又可以表示为$a^{2}+b^{2}+c^{2}+2ab + 2ac + 2bc$,所以$(a + b + c)^{2}=a^{2}+b^{2}+c^{2}+2ab + 2ac + 2bc$。
(2)$a^{2}+b^{2}+c^{2}=(a + b + c)^{2}-2ab - 2ac - 2bc = 10^{2}-2(ab + ac + bc)=100 - 2\times35 = 30$。
故答案为 30。
(3) 由题意可知,所拼图形的面积为$xa^{2}+yb^{2}+zab$。
因为$(5a + 7b)(9a + 4b)=45a^{2}+20ab + 63ab + 28b^{2}=45a^{2}+28b^{2}+83ab$,
所以$x = 45$,$y = 28$,$z = 83$,
所以$x + y + z=45 + 28 + 83 = 156$。
故答案为 156。
(1) 题图
(2)中图形的面积既可以表示为$(a + b + c)^{2}$,又可以表示为$a^{2}+b^{2}+c^{2}+2ab + 2ac + 2bc$,所以$(a + b + c)^{2}=a^{2}+b^{2}+c^{2}+2ab + 2ac + 2bc$。
(2)$a^{2}+b^{2}+c^{2}=(a + b + c)^{2}-2ab - 2ac - 2bc = 10^{2}-2(ab + ac + bc)=100 - 2\times35 = 30$。
故答案为 30。
(3) 由题意可知,所拼图形的面积为$xa^{2}+yb^{2}+zab$。
因为$(5a + 7b)(9a + 4b)=45a^{2}+20ab + 63ab + 28b^{2}=45a^{2}+28b^{2}+83ab$,
所以$x = 45$,$y = 28$,$z = 83$,
所以$x + y + z=45 + 28 + 83 = 156$。
故答案为 156。
查看更多完整答案,请扫码查看


