《2025年初中必刷题七年级数学下册苏科版》

1[2024江苏南京期中]下列各式中能用平方差公式计算的是　　　　　　　　　　　(　　　)
A. (a + 2)(a - 1)　　　
　B. (a - 2)(2 - a)
C. (a - 2)²　　　　　　
　D. (2 - a)(a + 2)

答案： D【解析】A选项，$(a + 2)(a - 1)$不能用平方差公式计算，故选项A不符合题意；B选项，$(a - 2)(2 - a)=-(a - 2)^2$，不能用平方差公式计算，故选项B不符合题意；C选项，$(a - 2)^2$不能用平方差公式计算，故选项C不符合题意；D选项，$(2 - a)(a + 2)=-(a - 2)(a + 2)$，能用平方差公式计算，故选项D符合题意. 故选D.

2[2024北京朝阳区质检]计算下列各式,结果是4y² - 1的是　　　　　　　　　　　　(　　　)
A. (-2y - 1)(-2y + 1)　
　B. (2y - 1)²
C. (4y - 1)²　　　　　
　D. (2y + 1)(-2y + 1)

答案： A【解析】A选项，$(-2y - 1)(-2y + 1)=4y^2 - 1$，故本选项符合题意；B选项，$(2y - 1)^2=4y^2 - 4y + 1$，故本选项不符合题意；C选项，$(4y - 1)^2=16y^2 - 8y + 1$，故本选项不符合题意；D选项，$(2y + 1)(-2y + 1)=1 - 4y^2$，故本选项不符合题意. 故选A.

3[2024江苏无锡期中]下列各式中计算正确的是　　　　　　　　　　　　　　　(　　　)
A. (a + m)(b + n) = ab + mn
B. (x + 1)(x - 1) = x² - 2x + 1
C. (x + 2)² = x² + 4
D. (-m + 2)(-m - 2) = m² - 4

答案： D【解析】A选项，$(a + m)(b + n)=ab + an + bm + mn$，原计算错误，不符合题意；B选项，$(x + 1)(x - 1)=x^2 - 1$，原计算错误，不符合题意；C选项，$(x + 2)^2=x^2 + 4x + 4$，原计算错误，不符合题意；D选项，$(-m + 2)(-m - 2)=m^2 - 4$，原计算正确，符合题意. 故选D.

4[2024江苏南通期中]若(m + 1)² = 3,(n + 1)² = 5,则(n + m + 2)(n - m)= ________.

答案： 2【解析】因为$(m + 1)^2=3$，$(n + 1)^2=5$，所以$m^2 + 2m + 1=3$，$n^2 + 2n + 1=5$，两等式相减，得$m^2 - n^2+2(m - n)= - 2$，所以$(n + m + 2)(n - m)=(n + m)(n - m)+2(n - m)=n^2 - m^2 - 2(m - n)=2$. 故答案为2.

5若a⁴ = 3,则(1 - a)(1 + a)(1 + a²)的值为________.

答案： -2【解析】原式$=(1 - a^2)(1 + a^2)=1 - a^4=1 - 3=-2$. 故答案为-2.

6[2024江苏南京期中]已知a＞0,b＞0,(3a + 3b + 1)(3a + 3b - 1)= 899,则a + b = ________.

答案： 10【解析】因为$(3a + 3b + 1)(3a + 3b - 1)=899$，所以$(3a + 3b)^2 - 1=899$，即$(3a + 3b)^2=900$. 又因为$(\pm30)^2=900$，$a＞0$，$b＞0$，所以$3a + 3b=30$，所以$a + b=10$. 故答案为10.

7新考法定义a※b = a(b + 1),例如2※3 = 2×(3 + 1)= 2×4 = 8,则(x - 1)※x的结果为________.

答案： $x^2 - 1$【解析】根据题意得$(x - 1)\otimes x=(x - 1)(x + 1)=x^2 - 1$. 故答案为$x^2 - 1$.

8我们知道,借助图形可以验证公式.下列图形可以用来验证平方差公式(a + b)(a - b)= a² - b²的是　　　　　　　　　　　　　　　(　　　)

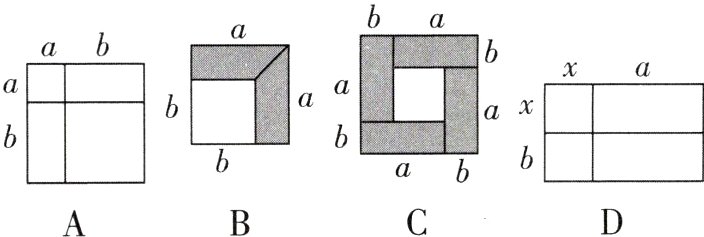
答案： B【解析】因为$(a + b)^2=a^2 + 2ab + b^2$，所以选项A不符合题意；因为$2\times\frac{1}{2}(a + b)(a - b)=a^2 - b^2$，所以选项B符合题意；因为$(a + b)^2-(a - b)^2=4ab$，所以选项C不符合题意；因为$(a + x)(b + x)=ab + ax + bx + x^2$，所以选项D不符合题意. 故选B.

9[2024江苏无锡期中]已知(a + 2b)² - (a - 2b)² = 8,则a与b的关系一定成立的是　　　(　　　)
A. a是b的相反数　　
　B. a是 - b的相反数
C. a是b的倒数　　　
　D. a是 - b的倒数

答案： C【解析】因为$(a + 2b)^2-(a - 2b)^2=8$，所以$[a + 2b+(a - 2b)][a + 2b-(a - 2b)]=2a\times4b=8$，所以$ab = 1$，即$a$是$b$的倒数. 故选C.

10[2023湖北武汉洪山区期末]若有理数满足(3x² + 2y² + 2023)(3x² + 2y² - 2023)= 1 - 2023²,则3x² + 2y²的值为________.

答案： 1【解析】因为$(3x^2 + 2y^2 + 2023)(3x^2 + 2y^2 - 2023)=1 - 2023^2$，所以$(3x^2 + 2y^2)^2 - 2023^2=1 - 2023^2$，所以$(3x^2 + 2y^2)^2=1$. 因为$3x^2 + 2y^2＞0$，所以$3x^2 + 2y^2=1$. 故答案为1.

11[2024江苏南京期中]某同学在计算3(4 + 1)(4² + 1)时,把3写成(4 - 1)后,发现可以连续运用平方差公式计算:3(4 + 1)(4² + 1)=(4 - 1)(4 + 1)(4² + 1)=(4² - 1)(4² + 1)= 16² - 1 = 255. 仿照该同学的计算方法,计算(1 + $\frac{1}{2}$)(1 + $\frac{1}{2^2}$)(1 + $\frac{1}{2^4}$)(1 + $\frac{1}{2^8}$)+ $\frac{1}{2^{15}}$的值为________.

答案： 2【解析】原式$=2(1-\frac{1}{2})(1 + \frac{1}{2})(1+\frac{1}{2^2})(1+\frac{1}{2^4})(1+\frac{1}{2^8})+\frac{1}{2^{15}}=2(1-\frac{1}{2^{16}})+\frac{1}{2^{15}}=2-\frac{1}{2^{15}}+\frac{1}{2^{15}}=2$.
方法点拨：简便计算时，考虑把相乘的两数转换成两个相同的数的和、差的形式，便于运用平方差公式；注意利用整体思想分组时，分出的两项要符合平方差公式的特征，不要出现符号错误。

12用平方差公式简便计算：
(1)98×102； (2)2021² - 2022×2020.

答案： 【解】
(1)$98\times102=(100 - 2)\times(100 + 2)=100^2 - 2^2=10000 - 4=9996$.
(2)原式$=2021^2-(2021 + 1)(2021 - 1)=2021^2-(2021^2 - 1^2)=2021^2 - 2021^2+1=1$.

13[2023江苏苏州期末]计算：
(1)(3 + 4y)(4y - 3) - (x - 4y)².
(2)(2a - 3b)² - (b + 3a)(3a - b).

答案： 【解】
(1)原式$=(4y + 3)(4y - 3)-(x - 4y)^2=16y^2 - 9-(x^2 - 8xy + 16y^2)=16y^2 - 9 - x^2 + 8xy - 16y^2=-9 - x^2 + 8xy$.
(2)原式$=4a^2 - 12ab + 9b^2-(9a^2 - b^2)=4a^2 - 12ab + 9b^2 + b^2 - 9a^2=10b^2 - 5a^2 - 12ab$.

14若(x + 2y)(x - 2y)= bx² - ay²,求(2a + b + 3)(2a + b - 3) - (2a + b)(2a - b)的值.

答案： 【解】由$(x + 2y)(x - 2y)=bx^2 - ay^2$，得$bx^2 - ay^2=x^2 - 4y^2$，则$a = 4$，$b = 1$. 原式$=[(2a + b)+3][(2a + b)-3]-(2a + b)(2a - b)=(2a + b)^2 - 9 - 4a^2 + b^2=4a^2 + 4ab + b^2 - 9 - 4a^2 + b^2=2b^2 + 4ab - 9$. 把$a = 4$，$b = 1$代入，得原式$=2\times1^2+4\times4\times1 - 9=9$.

15计算(x + 2y - z)(x - 2y + z)= ________.

答案： $x^2 - 4y^2 + 4yz - z^2$【解析】原式$=x^2-(2y - z)^2=x^2 - 4y^2 + 4yz - z^2$. 故答案为$x^2 - 4y^2 + 4yz - z^2$.