第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1[2024江苏宿迁调研,中]如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个人球孔,若一个球按图中所示的方向被击出(球可以经过多次反弹),则该球最后落入的球袋是( )
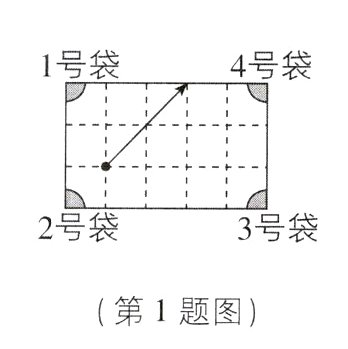
A. 1号袋
B. 2号袋
C. 3号袋
D. 4号袋

A. 1号袋
B. 2号袋
C. 3号袋
D. 4号袋
答案:
D【解析】如图所示,该球最后落入的球袋是 4 号袋. 故选 D.

D【解析】如图所示,该球最后落入的球袋是 4 号袋. 故选 D.

2[2024江苏扬州江都区期末,中]如图,将△ABC沿DE折叠,得到△A'DE,A'E,A'D与边BC分别相交于点M,N,若∠1 + ∠2 = 150°,则∠3 + ∠4的度数为( )
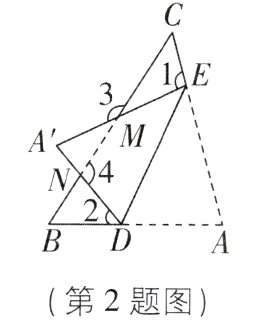
A. 250°
B. 255°
C. 260°
D. 265°

A. 250°
B. 255°
C. 260°
D. 265°
答案:
B【解析】由折叠得$\angle ADE = \angle A'DE$,$\angle AED = \angle A'ED$,所以$\angle 1 = 180^{\circ} - 2\angle AED$,$\angle 2 = 180^{\circ} - 2\angle ADE$,所以$\angle 1 + \angle 2 = 360^{\circ} - 2(\angle AED + \angle ADE) = 360^{\circ} - 2(180^{\circ} - \angle A) = 2\angle A$. 因为$\angle 1 + \angle 2 = 150^{\circ}$,所以$\angle A = 75^{\circ}$,所以$\angle B + \angle C = 180^{\circ} - \angle A = 105^{\circ}$. 因为$\angle 3 = 180^{\circ} - \angle CME = \angle 1 + \angle C$,$\angle 4 = 180^{\circ} - \angle BND = \angle 2 + \angle B$,所以$\angle 3 + \angle 4 = \angle 1 + \angle 2 + \angle B + \angle C = 150^{\circ} + 105^{\circ} = 255^{\circ}$,故选 B.
3[中]如图,在△ABC中,∠ACB = 90°,BC = 6,AC = 8,AB = 10,动点P在边AB上运动(不与端点重合),点P关于直线AC,BC对称的点分别为P₁,P₂,则在点P的运动过程中,线段P₁P₂的长的最小值是________.
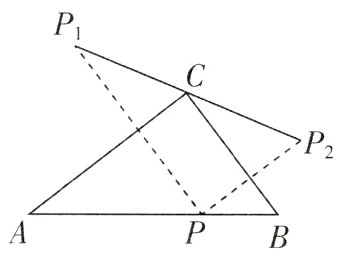

答案:
9.6
思路分析 利用轴对称的性质解决最值问题
连接$CP$,点$P$关于直线$AC$,$BC$对称的点分别为$P_1$,$P_2$
$CP_1 = CP = CP_2$;$P_1$,$C$,$P_2$三点共线
$P_1P_2 = 2CP$,求$CP$的最小值
由垂线段最短,转化为求$AB$边上的高
$S_{\triangle ABC} = \frac{1}{2}AB \cdot CP = \frac{1}{2}AC \cdot BC$,且$AB = 10$,$AC = 8$,$BC = 6$
【解析】连接$CP$.
因为点$P$关于直线$AC$,$BC$对称的点分别为$P_1$,$P_2$,所以$P_1C = PC = P_2C$,$\angle P_1CA = \angle PCA$,$\angle P_2CB = \angle PCB$,所以$\angle P_1CP_2 = 2\angle ACB = 180^{\circ}$,所以$P_1$,$C$,$P_2$三点共线,所以$P_1P_2 = 2CP$. 如图所示,当$CP \perp AB$时,$CP$的长最小,此时线段$P_1P_2$的长最小. 因为$\angle ACB = 90^{\circ}$,$BC = 6$,$AC = 8$,$AB = 10$,所以$CP = \frac{AC \times BC}{AB} = 4.8$,所以线段$P_1P_2$的长的最小值是 9.6.

9.6
思路分析 利用轴对称的性质解决最值问题
连接$CP$,点$P$关于直线$AC$,$BC$对称的点分别为$P_1$,$P_2$
$CP_1 = CP = CP_2$;$P_1$,$C$,$P_2$三点共线
$P_1P_2 = 2CP$,求$CP$的最小值
由垂线段最短,转化为求$AB$边上的高
$S_{\triangle ABC} = \frac{1}{2}AB \cdot CP = \frac{1}{2}AC \cdot BC$,且$AB = 10$,$AC = 8$,$BC = 6$
【解析】连接$CP$.
因为点$P$关于直线$AC$,$BC$对称的点分别为$P_1$,$P_2$,所以$P_1C = PC = P_2C$,$\angle P_1CA = \angle PCA$,$\angle P_2CB = \angle PCB$,所以$\angle P_1CP_2 = 2\angle ACB = 180^{\circ}$,所以$P_1$,$C$,$P_2$三点共线,所以$P_1P_2 = 2CP$. 如图所示,当$CP \perp AB$时,$CP$的长最小,此时线段$P_1P_2$的长最小. 因为$\angle ACB = 90^{\circ}$,$BC = 6$,$AC = 8$,$AB = 10$,所以$CP = \frac{AC \times BC}{AB} = 4.8$,所以线段$P_1P_2$的长的最小值是 9.6.

4[2023湖北广水校级期中,中](1)如图(1),P,Q分别是△ABC的边AB,AC上的两个定点,在边BC上找一点R,使△PQR的周长最小.
(2)如图(2),已知P是∠AOB内任意一点,分别在OA,OB上找点M,N,使△PMN的周长最小.
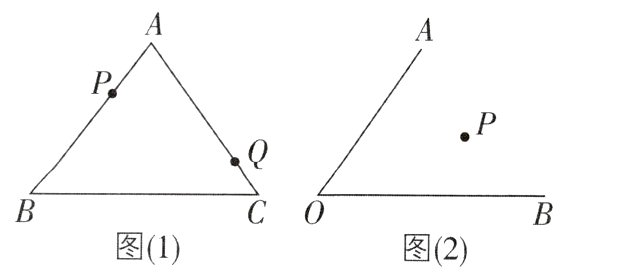
(2)如图(2),已知P是∠AOB内任意一点,分别在OA,OB上找点M,N,使△PMN的周长最小.

答案:
【解】
(1)如图
(1),点$R$即为所求. 作点$P$关于直线$BC$的对称点$P'$,连接$P'Q$交$BC$于$R$,此时$\triangle PQR$的周长最小.

(2)如图
(2),点$M$,$N$即为所求. 作$P$关于$OA$,$OB$的对称点$E$,$F$,连接$EF$交$OA$于$M$,交$OB$于$N$,此时$\triangle PMN$周长最小.

【解】
(1)如图
(1),点$R$即为所求. 作点$P$关于直线$BC$的对称点$P'$,连接$P'Q$交$BC$于$R$,此时$\triangle PQR$的周长最小.

(2)如图
(2),点$M$,$N$即为所求. 作$P$关于$OA$,$OB$的对称点$E$,$F$,连接$EF$交$OA$于$M$,交$OB$于$N$,此时$\triangle PMN$周长最小.

5[核心素养·几何直观][2024浙江绍兴嵊州期末,较难]如果两角之差的绝对值等于60°,则称这两个角互为“等差角”,即若|∠α - ∠β| = 60°,则称∠α和∠β互为“等差角”.(本题中所有角都是指大于0°,且小于180°的角)
(1)已知∠1和∠2互为“等差角”,若∠1 = 40°,则∠2 = ________;若∠1 = 90°,则∠2 = ________.
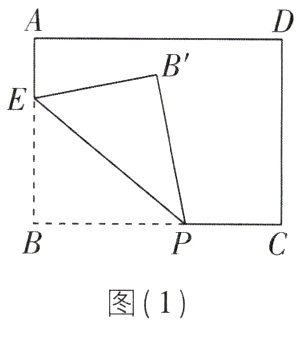
(2)如图(1),将一长方形纸片沿着EP翻折(点P在线段BC上,点E在线段AB上),点B落在点B'处. 若∠EPB'与∠B'PC互为“等差角”,求∠BPE的度数.
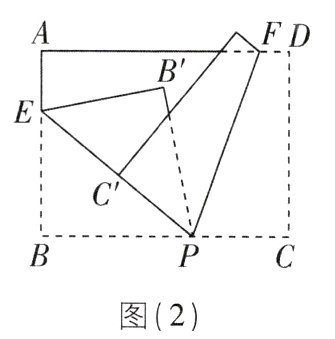
(3)再将纸片沿着FP翻折(点F在线段CD或AD上),点C落在点C'处. 如图(2),若点E,C',P在同一直线上,且∠B'PC'与∠EPF互为“等差角”,求∠EPF的度数(翻折后,线段PB'在∠EPF内部).
(1)已知∠1和∠2互为“等差角”,若∠1 = 40°,则∠2 = ________;若∠1 = 90°,则∠2 = ________.
(2)如图(1),将一长方形纸片沿着EP翻折(点P在线段BC上,点E在线段AB上),点B落在点B'处. 若∠EPB'与∠B'PC互为“等差角”,求∠BPE的度数.
(3)再将纸片沿着FP翻折(点F在线段CD或AD上),点C落在点C'处. 如图(2),若点E,C',P在同一直线上,且∠B'PC'与∠EPF互为“等差角”,求∠EPF的度数(翻折后,线段PB'在∠EPF内部).


答案:
【解】
(1)因为$\angle 1$和$\angle 2$互为“等差角”,$\angle 1 = 40^{\circ}$,所以$|40^{\circ} - \angle 2| = 60^{\circ}$,所以$40^{\circ} - \angle 2 = 60^{\circ}$或$40^{\circ} - \angle 2 = -60^{\circ}$,解得$\angle 2 = -20^{\circ}$(舍去)或$100^{\circ}$.
因为$\angle 1$和$\angle 2$互为“等差角”,$\angle 1 = 90^{\circ}$,所以$|90^{\circ} - \angle 2| = 60^{\circ}$,所以$90^{\circ} - \angle 2 = 60^{\circ}$或$90^{\circ} - \angle 2 = -60^{\circ}$,解得$\angle 2 = 30^{\circ}$或$150^{\circ}$. 故答案为$100^{\circ}$,$30^{\circ}$或$150^{\circ}$.
(2)因为$\angle EPB'$与$\angle B'PC$互为“等差角”,所以当$\angle EPB' < \angle B'PC$时,$\angle B'PC - \angle EPB' = 60^{\circ}$,所以$\angle B'PC = \angle EPB' + 60^{\circ}$.
因为$\triangle BEP$翻折得$\triangle B'EP$,所以$\angle EPB = \angle EPB'$. 因为$\angle EPB + \angle EPB' + \angle B'PC = 180^{\circ}$,所以$\angle EPB' + \angle EPB' + \angle EPB' + 60^{\circ} = 180^{\circ}$,解得$\angle EPB' = 40^{\circ}$. 当$\angle EPB' > \angle B'PC$时,$\angle EPB' - \angle B'PC = 60^{\circ}$,同理可得$\angle EPB' = 80^{\circ}$.
综上所述,$\angle EPB$的度数为$40^{\circ}$或$80^{\circ}$.
(3)因为点$E$,$C'$,$P$在同一直线上,且$\angle B'PC'$与$\angle EPF$互为“等差角”,$\angle B'PC' < \angle EPF$,所以$\angle EPF - \angle B'PC' = 60^{\circ}$,所以$\angle BPE = \angle B'PE = \angle EPF - 60^{\circ}$.
因为$\angle FPC = \angle EPF$,$\angle BPE + \angle EPF + \angle FPC = 180^{\circ}$,所以$\angle EPF - 60^{\circ} + \angle EPF + \angle EPF = 180^{\circ}$,所以$\angle EPF = 80^{\circ}$.
关键点拨
掌握轴对称的性质及两点之间线段最短是解题的关键.
归纳总结
本题考查旋转的相关知识:
(1)旋转前后的两个图形对应线段、对应角分别相等,图形的大小、形状都不改变.
(2)旋转的三要素:①定点——旋转中心;②旋转方向;③旋转角. 判断能否构成旋转,关键是看有没有旋转中心、旋转方向和旋转角.
(1)因为$\angle 1$和$\angle 2$互为“等差角”,$\angle 1 = 40^{\circ}$,所以$|40^{\circ} - \angle 2| = 60^{\circ}$,所以$40^{\circ} - \angle 2 = 60^{\circ}$或$40^{\circ} - \angle 2 = -60^{\circ}$,解得$\angle 2 = -20^{\circ}$(舍去)或$100^{\circ}$.
因为$\angle 1$和$\angle 2$互为“等差角”,$\angle 1 = 90^{\circ}$,所以$|90^{\circ} - \angle 2| = 60^{\circ}$,所以$90^{\circ} - \angle 2 = 60^{\circ}$或$90^{\circ} - \angle 2 = -60^{\circ}$,解得$\angle 2 = 30^{\circ}$或$150^{\circ}$. 故答案为$100^{\circ}$,$30^{\circ}$或$150^{\circ}$.
(2)因为$\angle EPB'$与$\angle B'PC$互为“等差角”,所以当$\angle EPB' < \angle B'PC$时,$\angle B'PC - \angle EPB' = 60^{\circ}$,所以$\angle B'PC = \angle EPB' + 60^{\circ}$.
因为$\triangle BEP$翻折得$\triangle B'EP$,所以$\angle EPB = \angle EPB'$. 因为$\angle EPB + \angle EPB' + \angle B'PC = 180^{\circ}$,所以$\angle EPB' + \angle EPB' + \angle EPB' + 60^{\circ} = 180^{\circ}$,解得$\angle EPB' = 40^{\circ}$. 当$\angle EPB' > \angle B'PC$时,$\angle EPB' - \angle B'PC = 60^{\circ}$,同理可得$\angle EPB' = 80^{\circ}$.
综上所述,$\angle EPB$的度数为$40^{\circ}$或$80^{\circ}$.
(3)因为点$E$,$C'$,$P$在同一直线上,且$\angle B'PC'$与$\angle EPF$互为“等差角”,$\angle B'PC' < \angle EPF$,所以$\angle EPF - \angle B'PC' = 60^{\circ}$,所以$\angle BPE = \angle B'PE = \angle EPF - 60^{\circ}$.
因为$\angle FPC = \angle EPF$,$\angle BPE + \angle EPF + \angle FPC = 180^{\circ}$,所以$\angle EPF - 60^{\circ} + \angle EPF + \angle EPF = 180^{\circ}$,所以$\angle EPF = 80^{\circ}$.
关键点拨
掌握轴对称的性质及两点之间线段最短是解题的关键.
归纳总结
本题考查旋转的相关知识:
(1)旋转前后的两个图形对应线段、对应角分别相等,图形的大小、形状都不改变.
(2)旋转的三要素:①定点——旋转中心;②旋转方向;③旋转角. 判断能否构成旋转,关键是看有没有旋转中心、旋转方向和旋转角.
查看更多完整答案,请扫码查看


