第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
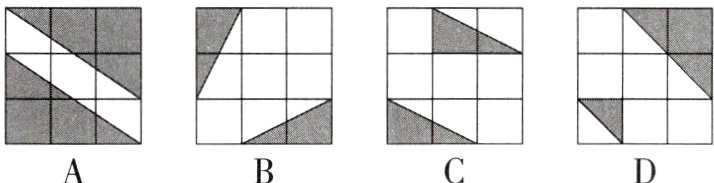
1[2024湖北武汉黄陂区模拟]下列每个正方形网格中均有两个图形,其中一个图形可以由另一个进行轴对称变换得到的是( )

答案:
B【解析】A选项,不可以通过轴对称变换得到,故此选项错误;B选项,可以通过轴对称变换得到,故此选项正确;C选项,不可以通过轴对称变换得到,故此选项错误;D选项不可以通过轴对称变换得到,故此选项错误. 故选B.
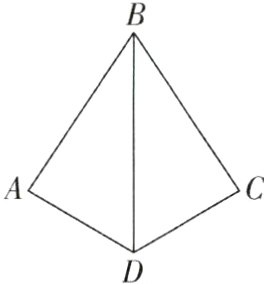
2[2024江苏南京调研]如图,若将四边形ABCD沿直线BD对折后,△ABD和△CBD重合,则AB的对应边是________,BD的对应边是________,∠ADB的对应角是________.

答案:
CB BD ∠CDB【解析】因为将四边形AB - CD沿直线BD对折后,△ABD和△CBD重合,所以△ABD与△CBD关于BD所在直线对称,所以AB的对应边是CB,BD的对应边是BD,∠ADB的对应角是∠CDB,故答案为CB,BD,∠CDB.
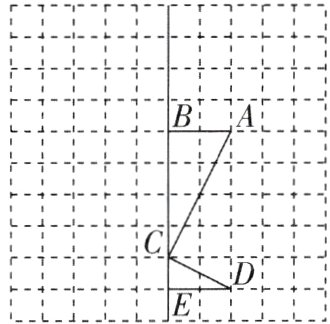
3[2024江苏泰州期末]在如图所示的正方形网格中画出所给图形关于直线BE对称的图形,点A,D的对应点分别为点A₁,D₁.

答案:
【解】如图所示.

【解】如图所示.

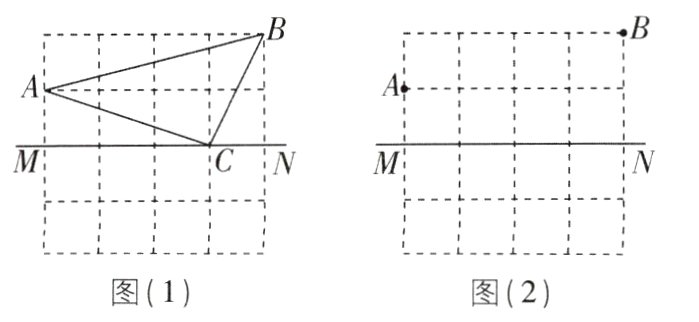
4[2024浙江杭州拱墅区期末]如图,在正方形网格中,点A,B,C均为网格线交点.
(1)如图(1),作出△ABC关于直线MN对称的图形;
(2)如图(2),在直线MN上求作点P,使得∠APM = ∠BPN.
(1)如图(1),作出△ABC关于直线MN对称的图形;
(2)如图(2),在直线MN上求作点P,使得∠APM = ∠BPN.

答案:
【解】
(1)如图
(1),△A'B'C即为所求.


(2)如图
(2),点P即为所求.
【解】
(1)如图
(1),△A'B'C即为所求.


(2)如图
(2),点P即为所求.
5下列说法错误的是( )
A. 过线段的中点且垂直于该条线段的直线是线段的垂直平分线
B. 线段的垂直平分线垂直于该线段
C. 过线段上的一点且垂直于线段的直线是线段的垂直平分线
D. 线段的垂直平分线平分该线段
A. 过线段的中点且垂直于该条线段的直线是线段的垂直平分线
B. 线段的垂直平分线垂直于该线段
C. 过线段上的一点且垂直于线段的直线是线段的垂直平分线
D. 线段的垂直平分线平分该线段
答案:
C【解析】过线段的中点且垂直于该条线段的直线是线段的垂直平分线,故A选项的说法正确,C选项的说法错误;线段的垂直平分线既垂直于该线段,又平分该线段,故B、D选项的说法正确. 故选C.
6[2024陕西西安期末改编]如图,P是∠AOB的边OB上一点.
(1)在图(1)中用直尺和圆规过点P作OA的垂线,垂足为H;
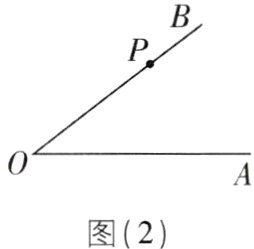
(2)在图(2)中用直尺和圆规过点P作OB的垂线,交OA于点C.
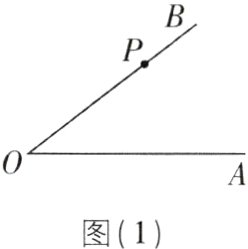
(1)在图(1)中用直尺和圆规过点P作OA的垂线,垂足为H;
(2)在图(2)中用直尺和圆规过点P作OB的垂线,交OA于点C.


答案:
【解】
(1)如图
(1),PH即为所求.
关键点拨
此题主要考查了轴对称的性质,熟知成轴对称的两个图形中,不在对称轴上的两个对应点的连线段被对称轴垂直平分及三角形的三边关系是解题的关键.
思路分析
(2)作点A关于MN的对称点A',连接A'B,A'B与MN的交点即为所求.
(2)如图
(2),PC即为所求.


【解】
(1)如图
(1),PH即为所求.
关键点拨
此题主要考查了轴对称的性质,熟知成轴对称的两个图形中,不在对称轴上的两个对应点的连线段被对称轴垂直平分及三角形的三边关系是解题的关键.
思路分析
(2)作点A关于MN的对称点A',连接A'B,A'B与MN的交点即为所求.
(2)如图
(2),PC即为所求.


7[2024江苏南京校级期末]如图,已知射线AD平分∠BAC.
(1)请用尺规作出BC的垂直平分线,交AD于点P,交BC于点Q,交AB于点R,不写作法,保留作图痕迹;
(2)若∠B = 30°,∠C = 50°,求∠DPQ的度数.
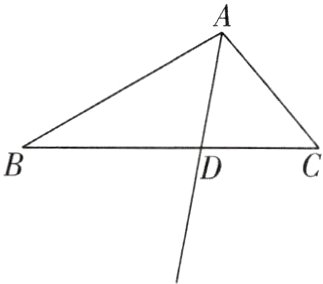
(1)请用尺规作出BC的垂直平分线,交AD于点P,交BC于点Q,交AB于点R,不写作法,保留作图痕迹;
(2)若∠B = 30°,∠C = 50°,求∠DPQ的度数.

答案:
【解】
(1)如图所示,直线RQ即为所求.
(2)因为∠B = 30°,∠C = 50°,所以∠BAC = 180° - 30° - 50° = 100°.
因为AD平分∠BAC,
所以∠CAD = $\frac{1}{2}$∠BAC = 50°,
所以∠ADC = 180° - 50° - 50° = 80°,
所以∠PDQ = ∠ADC = 80°.
因为QR垂直平分BC,所以∠PQD = 90°,所以∠DPQ = 180° - 90° - 80° = 10°.

【解】
(1)如图所示,直线RQ即为所求.
(2)因为∠B = 30°,∠C = 50°,所以∠BAC = 180° - 30° - 50° = 100°.
因为AD平分∠BAC,
所以∠CAD = $\frac{1}{2}$∠BAC = 50°,
所以∠ADC = 180° - 50° - 50° = 80°,
所以∠PDQ = ∠ADC = 80°.
因为QR垂直平分BC,所以∠PQD = 90°,所以∠DPQ = 180° - 90° - 80° = 10°.

查看更多完整答案,请扫码查看


