第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1 下列方程中:①$x + y + z = 3$;②$xyz = 3$;③$\frac{x + y + z}{3}=1$;④$\frac{3}{x + y + z}=1$. 三元一次方程共有( )
A. 1个
B. 2个
C. 3个
D. 4个
A. 1个
B. 2个
C. 3个
D. 4个
答案:
1. B 【解析】①$x + y + z = 3$是三元一次方程;②$xyz = 3$不是三元一次方程;③$\frac{x + y + z}{3} = 1$是三元一次方程;④$\frac{3}{x + y + z} = 1$不是三元一次方程,则三元一次方程共有2个. 故选B.
2 [2023江苏宿迁调研]若方程组$\begin{cases}x - by + 4z = 1,\\x - 2by + 3z = 3\end{cases}$的解是$\begin{cases}x = a,\\y = 1,\\z = c,\end{cases}$则$a + b + 6c$的值是( )
A. -3
B. 0
C. 3
D. 6
A. -3
B. 0
C. 3
D. 6
答案:
2. A 【解析】把$\begin{cases}x = a\\y = 1\\z = c\end{cases}$代入方程组得$\begin{cases}a - b + 4c = 1,①\\a - 2b + 3c = 3,②\end{cases}$① - ②得$b + c = - 2$,即$b = - 2 - c$,①×2 - ②得$a + 5c = - 1$,即$a = - 5c - 1$,则原式$= - 5c - 1 - 2 - c + 6c = - 3$. 故选A.
3 [2024福建泉州质检]方程组$\begin{cases}x + y = 1,\\x + z = 0,\\y + z = -1\end{cases}$的解是( )
A. $\begin{cases}x = -1,\\y = 1,\\z = 0\end{cases}$
B. $\begin{cases}x = 1,\\y = 0,\\z = -1\end{cases}$
C. $\begin{cases}x = 0,\\y = 1,\\z = -1\end{cases}$
D. $\begin{cases}x = -1,\\y = 0,\\z = 1\end{cases}$
A. $\begin{cases}x = -1,\\y = 1,\\z = 0\end{cases}$
B. $\begin{cases}x = 1,\\y = 0,\\z = -1\end{cases}$
C. $\begin{cases}x = 0,\\y = 1,\\z = -1\end{cases}$
D. $\begin{cases}x = -1,\\y = 0,\\z = 1\end{cases}$
答案:
3. B 【解析】$\begin{cases}x + y = 1,①\\x + z = 0,②\\y + z = - 1,③\end{cases}$① + ② + ③,得$2x + 2y + 2z = 0$,即$x + y + z = 0$,④ 将①代入④,得$z = - 1$,将②代入④,得$y = 0$,将③代入④,得$x = 1$,所以方程组的解为$\begin{cases}x = 1\\y = 0\\z = - 1\end{cases}$,故选B.
解三元一次方程组的基本思路:
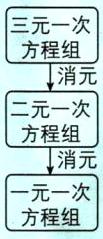
关键点拨:把$x$,$y$与$z$的值代入方程组,将$c$看成已知数表示出$a$与$b$,再代入原式计算即可求出代数式的值.
3. B 【解析】$\begin{cases}x + y = 1,①\\x + z = 0,②\\y + z = - 1,③\end{cases}$① + ② + ③,得$2x + 2y + 2z = 0$,即$x + y + z = 0$,④ 将①代入④,得$z = - 1$,将②代入④,得$y = 0$,将③代入④,得$x = 1$,所以方程组的解为$\begin{cases}x = 1\\y = 0\\z = - 1\end{cases}$,故选B.
解三元一次方程组的基本思路:

关键点拨:把$x$,$y$与$z$的值代入方程组,将$c$看成已知数表示出$a$与$b$,再代入原式计算即可求出代数式的值.
4 [2023北京朝阳区质检]小铃观察三元一次方程组$\begin{cases}x + y + z = 1,①\\4x + 2y + z = 3,②\\9x + 3y + z = 7③\end{cases}$各个未知数的系数特点,先用② - ①,得$3x + y = 2$,记为④,消掉未知数$z$,那么下一步应完成的是________,得到________,记为⑤,由④⑤可解得$x$,$y$的值,通过代入$x$,$y$的值求出未知数$z$的值,完成这个三元一次方程组的求解.
答案:
4. ③ - ① $8x + 2y = 6$(本题答案不唯一)
【解析】$\begin{cases}x + y + z = 1,①\\4x + 2y + z = 3,②\\9x + 3y + z = 7,③\end{cases}$② - ①,得$3x + y = 2$,④ ③ - ①,得$8x + 2y = 6$,⑤ 由④⑤得到二元一次方程组$\begin{cases}3x + y = 2\\8x + 2y = 6\end{cases}$,解得$\begin{cases}x = 1\\y = - 1\end{cases}$,把$\begin{cases}x = 1\\y = - 1\end{cases}$代入①得$z = 1$,所以原方程组的解为$\begin{cases}x = 1\\y = - 1\\z = 1\end{cases}$,故答案为③ - ①,$8x + 2y = 6$. (本题答案不唯一)
【解析】$\begin{cases}x + y + z = 1,①\\4x + 2y + z = 3,②\\9x + 3y + z = 7,③\end{cases}$② - ①,得$3x + y = 2$,④ ③ - ①,得$8x + 2y = 6$,⑤ 由④⑤得到二元一次方程组$\begin{cases}3x + y = 2\\8x + 2y = 6\end{cases}$,解得$\begin{cases}x = 1\\y = - 1\end{cases}$,把$\begin{cases}x = 1\\y = - 1\end{cases}$代入①得$z = 1$,所以原方程组的解为$\begin{cases}x = 1\\y = - 1\\z = 1\end{cases}$,故答案为③ - ①,$8x + 2y = 6$. (本题答案不唯一)
5 [2024上海静安区期末]解方程组:
(1)$\begin{cases}-6x + 5y - 3z = -4,\\6x - 3y + z = 8,\\6x + y + 4z = 9;\end{cases}$
(2)$\begin{cases}x - y - z = 2,\\3x + 5y + 7z = 24,\\4x - y + 2z = 26.\end{cases}$
(1)$\begin{cases}-6x + 5y - 3z = -4,\\6x - 3y + z = 8,\\6x + y + 4z = 9;\end{cases}$
(2)$\begin{cases}x - y - z = 2,\\3x + 5y + 7z = 24,\\4x - y + 2z = 26.\end{cases}$
答案:
5. 【解】
(1)$\begin{cases}- 6x + 5y - 3z = - 4,①\\6x - 3y + z = 8,②\\6x + y + 4z = 9,③\end{cases}$
① + ②,得$2y - 2z = 4$,整理得$y - z = 2$,④
① + ③,得$6y + z = 5$,⑤
联立④⑤解得$\begin{cases}y = 1\\z = - 1\end{cases}$
把$\begin{cases}y = 1\\z = - 1\end{cases}$代入②,得$x = 2$,所以原方程组的解为$\begin{cases}x = 2\\y = 1\\z = - 1\end{cases}$
(2)$\begin{cases}x - y - z = 2,①\\3x + 5y + 7z = 24,②\\4x - y + 2z = 26,③\end{cases}$
③ - ①,得$3x + 3z = 24$,整理得$x + z = 8$,④
①×5 + ②,得$8x + 2z = 34$,整理得$4x + z = 17$,⑤
联立④⑤解得$\begin{cases}x = 3\\z = 5\end{cases}$,把$\begin{cases}x = 3\\z = 5\end{cases}$代入①,得$y = - 4$,所以原方程组的解为$\begin{cases}x = 3\\y = - 4\\z = 5\end{cases}$
(1)$\begin{cases}- 6x + 5y - 3z = - 4,①\\6x - 3y + z = 8,②\\6x + y + 4z = 9,③\end{cases}$
① + ②,得$2y - 2z = 4$,整理得$y - z = 2$,④
① + ③,得$6y + z = 5$,⑤
联立④⑤解得$\begin{cases}y = 1\\z = - 1\end{cases}$
把$\begin{cases}y = 1\\z = - 1\end{cases}$代入②,得$x = 2$,所以原方程组的解为$\begin{cases}x = 2\\y = 1\\z = - 1\end{cases}$
(2)$\begin{cases}x - y - z = 2,①\\3x + 5y + 7z = 24,②\\4x - y + 2z = 26,③\end{cases}$
③ - ①,得$3x + 3z = 24$,整理得$x + z = 8$,④
①×5 + ②,得$8x + 2z = 34$,整理得$4x + z = 17$,⑤
联立④⑤解得$\begin{cases}x = 3\\z = 5\end{cases}$,把$\begin{cases}x = 3\\z = 5\end{cases}$代入①,得$y = - 4$,所以原方程组的解为$\begin{cases}x = 3\\y = - 4\\z = 5\end{cases}$
6 已知方程组$\begin{cases}x + 2y = k,\\2x + y = 1\end{cases}$的解满足$x + y = 3$,则$k$的值为( )
A. 10
B. 8
C. 2
D. -8
A. 10
B. 8
C. 2
D. -8
答案:
6. B 【解析】由题意可得$\begin{cases}x + 2y = k,①\\2x + y = 1,②\\x + y = 3.③\end{cases}$2×① - ②得$y = \frac{2}{3}k - \frac{1}{3}$,② - ③得$x = - 2$. 将$x = - 2$代入③得$y = 5$,则$\frac{2}{3}k - \frac{1}{3} = 5$,解得$k = 8$. 故选B.
7 [2023江苏扬州广陵区质检]三个二元一次方程$2x + 5y - 6 = 0$,$3x - 2y - 9 = 0$,$y = kx - 9$有公共解,则$k$的值是________.
答案:
7. 3 【解析】由题意得$\begin{cases}2x + 5y - 6 = 0,①\\3x - 2y - 9 = 0,②\\y = kx - 9,③\end{cases}$
①×3 - ②×2得$y = 0$. 将$y = 0$代入①得$x = 3$. 把$x = 3$,$y = 0$代入③,得$3k - 9 = 0$,解得$k = 3$. 故答案为3.
①×3 - ②×2得$y = 0$. 将$y = 0$代入①得$x = 3$. 把$x = 3$,$y = 0$代入③,得$3k - 9 = 0$,解得$k = 3$. 故答案为3.
8 有甲、乙、丙三种货物,若购买甲3件、乙7件、丙1件,共300元;若购买甲4件、乙9件、丙1件,共420元. 现在购买甲1件、乙2件,共需________元.
答案:
8. 120 【解析】设购买甲、乙、丙各1件分别需要$x$,$y$,$z$元. 根据题意,得$\begin{cases}3x + 7y + z = 300,①\\4x + 9y + z = 420.②\end{cases}$
② - ①得$x + 2y = 120$,即现在购买甲1件、乙2件,共需120元.
② - ①得$x + 2y = 120$,即现在购买甲1件、乙2件,共需120元.
9 已知$y = ax^{2}+bx + c$,当$x = 1$时,$y = 8$;当$x = 0$时,$y = 2$;当$x = -2$时,$y = 4$.
(1)求$a$,$b$,$c$的值;
(2)当$x = -3$时,求$y$的值.
(1)求$a$,$b$,$c$的值;
(2)当$x = -3$时,求$y$的值.
答案:
9. 【解】
(1)根据题意得$\begin{cases}a + b + c = 8,①\\c = 2,②\\4a - 2b + c = 4.③\end{cases}$
把②代入①,得$a + b + 2 = 8$. ④
把②代入③,得$4a - 2b + 2 = 4$. ⑤
由④和⑤组成方程组$\begin{cases}a + b + 2 = 8\\4a - 2b + 2 = 4\end{cases}$,
解得$a = \frac{7}{3}$,$b = \frac{11}{3}$,
所以$a = \frac{7}{3}$,$b = \frac{11}{3}$,$c = 2$.
(2)由
(1)得$y = \frac{7}{3}x^{2} + \frac{11}{3}x + 2$.
当$x = - 3$时,$y = \frac{7}{3}×(- 3)^{2} + \frac{11}{3}×(- 3) + 2 = 12$.
(1)根据题意得$\begin{cases}a + b + c = 8,①\\c = 2,②\\4a - 2b + c = 4.③\end{cases}$
把②代入①,得$a + b + 2 = 8$. ④
把②代入③,得$4a - 2b + 2 = 4$. ⑤
由④和⑤组成方程组$\begin{cases}a + b + 2 = 8\\4a - 2b + 2 = 4\end{cases}$,
解得$a = \frac{7}{3}$,$b = \frac{11}{3}$,
所以$a = \frac{7}{3}$,$b = \frac{11}{3}$,$c = 2$.
(2)由
(1)得$y = \frac{7}{3}x^{2} + \frac{11}{3}x + 2$.
当$x = - 3$时,$y = \frac{7}{3}×(- 3)^{2} + \frac{11}{3}×(- 3) + 2 = 12$.
10 [2024湖北武汉质检]在$\triangle ABC$中,$\angle B = 2\angle C$,$\angle A$比$\angle C$多$20^{\circ}$,求$\triangle ABC$各内角度数.
答案:
10. 【解】由题意,得$\begin{cases}\angle A+\angle B+\angle C = 180^{\circ},①\\\angle B = 2\angle C,②\\\angle A = \angle C + 20^{\circ},③\end{cases}$
将②③代入①,解得$\angle C = 40^{\circ}$,
将$\angle C = 40^{\circ}$代入②,得$\angle B = 80^{\circ}$,
将$\angle C = 40^{\circ}$代入③,得$\angle A = 60^{\circ}$,
所以$\triangle ABC$各内角度数为$\angle A = 60^{\circ}$,$\angle B = 80^{\circ}$,$\angle C = 40^{\circ}$.
将②③代入①,解得$\angle C = 40^{\circ}$,
将$\angle C = 40^{\circ}$代入②,得$\angle B = 80^{\circ}$,
将$\angle C = 40^{\circ}$代入③,得$\angle A = 60^{\circ}$,
所以$\triangle ABC$各内角度数为$\angle A = 60^{\circ}$,$\angle B = 80^{\circ}$,$\angle C = 40^{\circ}$.
查看更多完整答案,请扫码查看


